Дано линейное уравнение
\(\displaystyle 3{,}33(x+2,56)=3\frac{3}{25}+\frac{7}{3}x\)
и график линейной функции
\(\displaystyle y=3{,}33(x+2,56)-3\frac{3}{25}-\frac{7}{3}x.\)
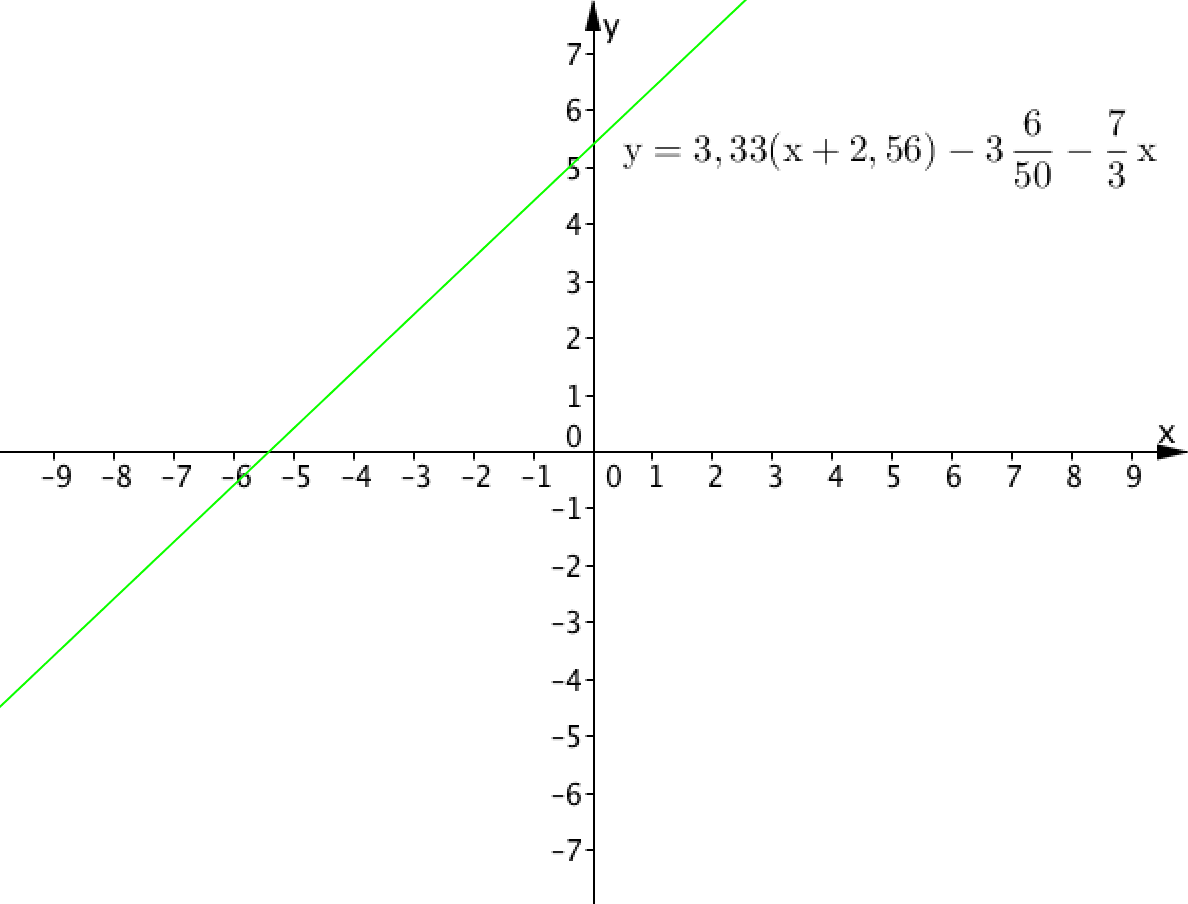
Определите число решений данного линейного уравнения.
Первая координата (абсцисса) точки пересечения прямой \(\displaystyle y=3{,}33(x+2{,}56)-3\frac{3}{25}-\frac{7}{3}x\) с осью \(\displaystyle OX\) является решением линейного уравнения
\(\displaystyle 3{,}33(x+2{,}56)-3\frac{3}{25}-\frac{7}{3}x=0{\small ,}\)
или, если перенести \(\displaystyle -3\frac{3}{25}-\frac{7}{3}x\) вправо с противоположными знаками,
\(\displaystyle 3{,}33(x+2{,}56)=3\frac{3}{25}+\frac{7}{3}x{\small .}\)
Поэтому число точек пересечения прямой
\(\displaystyle y=3{,}33(x+2{,}56)-3\frac{3}{25}-\frac{7}{3}x\)
с осью \(\displaystyle OX\) совпадает с числом решений линейного уравнения
\(\displaystyle 3{,}33(x+2{,}56)=3\frac{3}{25}+\frac{7}{3}x{\small .}\)
Из графика видно, что прямая пересекает ось \(\displaystyle OX\) только в одной точке, то есть линейное уравнение имеет одно решение.
Ответ: одно решение.