Не прибегая к вычислениям, решите линейное уравнение
\(\displaystyle 2x+\frac{6x-5}{7}-\frac{8x+7}{3}=0,\)
если известен график линейной функции
\(\displaystyle y=2x+\frac{6x-5}{7}-\frac{8x+7}{3}.\)
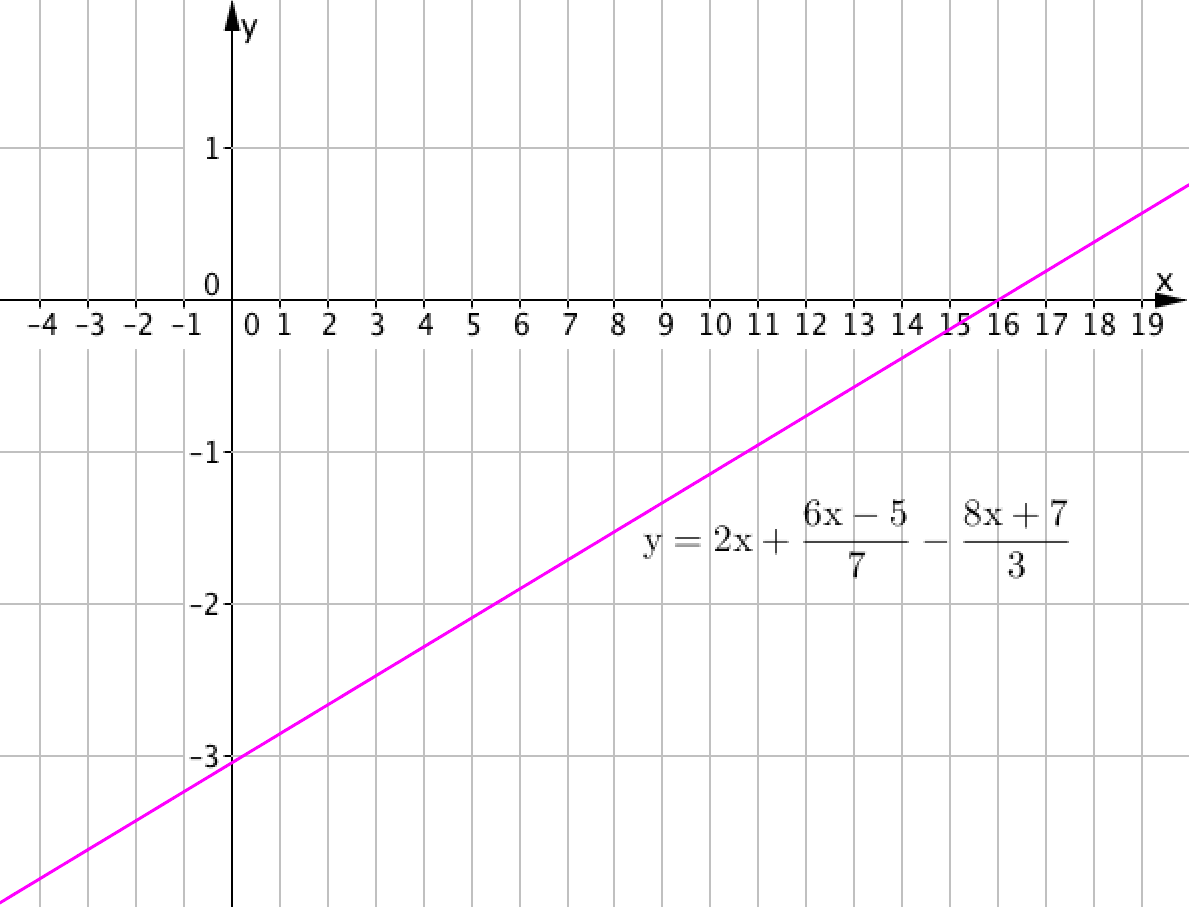
\(\displaystyle x=\)
Точка пересечения прямой \(\displaystyle y=2x+\frac{6x-5}{7}-\frac{8x+7}{3}\) с осью \(\displaystyle OX\) (ось абсцисс) имеет координату \(\displaystyle (x_{0};0),\) где \(\displaystyle x_{0}\) – решение линейного уравнения \(\displaystyle 2x+\frac{6x-5}{7}-\frac{8x+7}{3}=0.\)
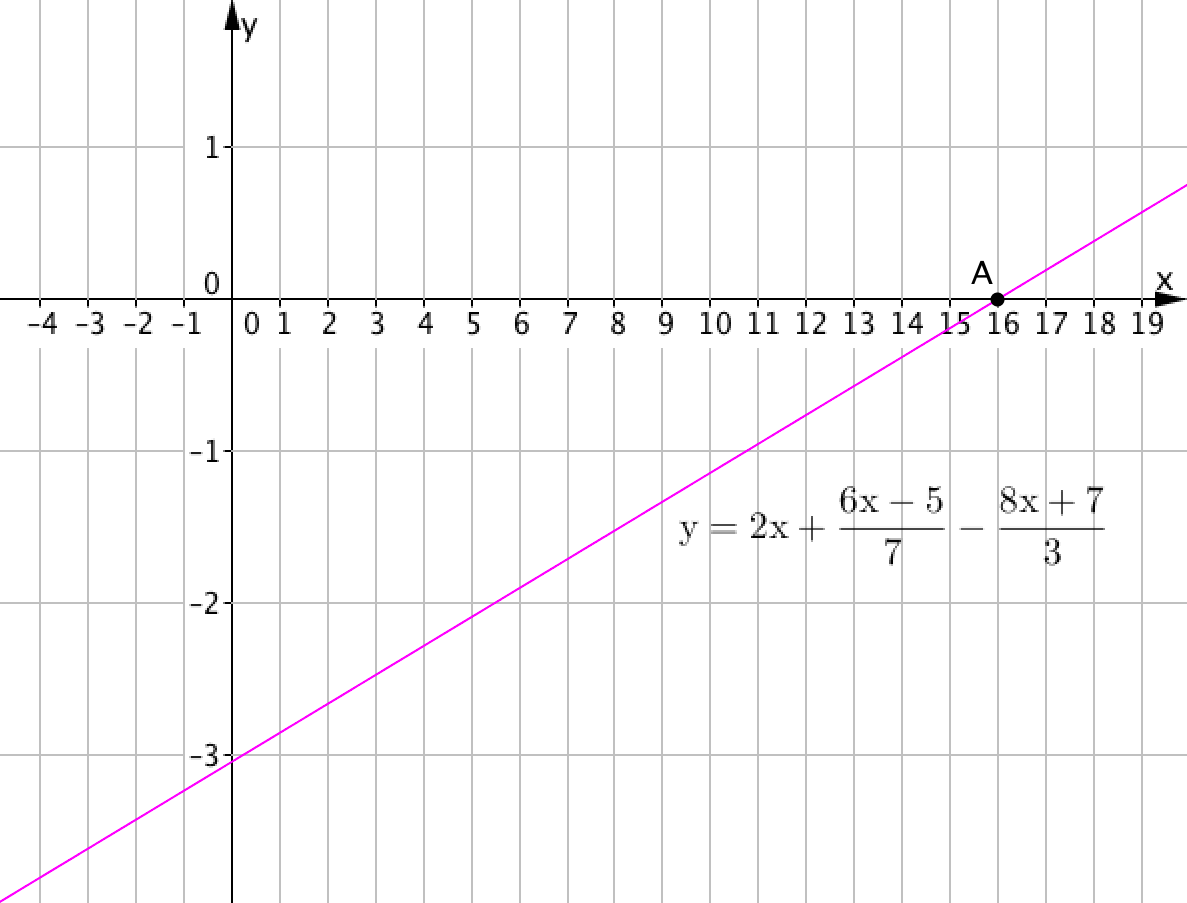
Из рисунка видно, что график линейной функции \(\displaystyle y=2x+\frac{6x-5}{7}-\frac{8x+7}{3}\) пересекает ось \(\displaystyle OX\) в точке \(\displaystyle A\,(16;0)\) с абсциссой \(\displaystyle x=16.\)
Поэтому \(\displaystyle x=16\) является корнем линейного уравнения \(\displaystyle 2x+\frac{6x-5}{7}-\frac{8x+7}{3}=0.\)
Ответ: \(\displaystyle x=16.\)