Найдите координаты точки \(\displaystyle A\) пересечения прямой
\(\displaystyle y=\frac{3}{5}x+\frac{1}{7}\)
с осью \(\displaystyle OX,\) решив соответствующее линейное уравнение:
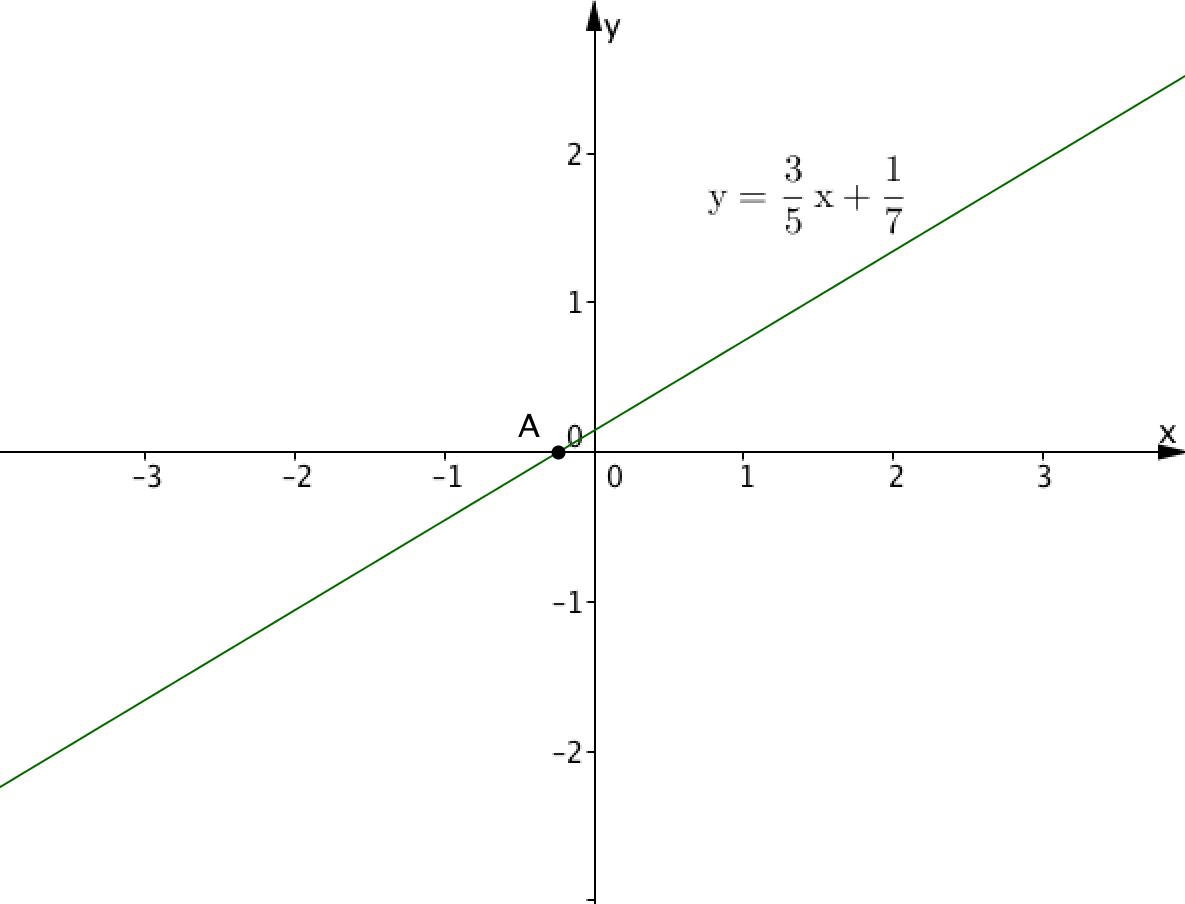
Точка \(\displaystyle A(x_{0};y_{0})\) является точкой пересечения прямой \(\displaystyle y=\frac{3}{5}x+\frac{1}{7}\) с осью \(\displaystyle OX.\)
Поэтому:
- координата \(\displaystyle y_{0}=0,\)
-
координата \(\displaystyle x_{0}\) является решением линейного уравнения \(\displaystyle \frac{3}{5}x+\frac{1}{7}=0,\)
которое получается из пересечения прямой \(\displaystyle y=\frac{3}{5}x+\frac{1}{7}\) с осью \(\displaystyle OX.\)
Решим линейное уравнение:
\(\displaystyle \frac{3}{5}x+\frac{1}{7}=0.\)
Перенесем \(\displaystyle \frac{1}{7}\) в правую часть уравнения с противоположным знаком:
\(\displaystyle \frac{3}{5}x=-\frac{1}{7}.\)
Разделим обе части уравнения на \(\displaystyle \frac{3}{5}\):
\(\displaystyle \frac{3}{5}x:\frac{3}{5}=\left(-\frac{1}{7}\right):\frac{3}{5},\)
\(\displaystyle x=\left(-\frac{1}{7}\right)\cdot \frac{5}{3},\)
\(\displaystyle x=-\frac{5}{21}.\)
Таким образом, координата
\(\displaystyle x_{0}=-\frac{5}{21},\)
и точка \(\displaystyle A\) имеет координаты
\(\displaystyle \left(-\frac{5}{21};0 \right).\)
Ответ: \(\displaystyle \left(-\frac{5}{21};0 \right).\)