Дано линейное уравнение:
\(\displaystyle -4x+12=0.\)
Какая из изображенных на рисунке прямых при пересечении с осью \(\displaystyle OX\) дает заданное линейное уравнение?
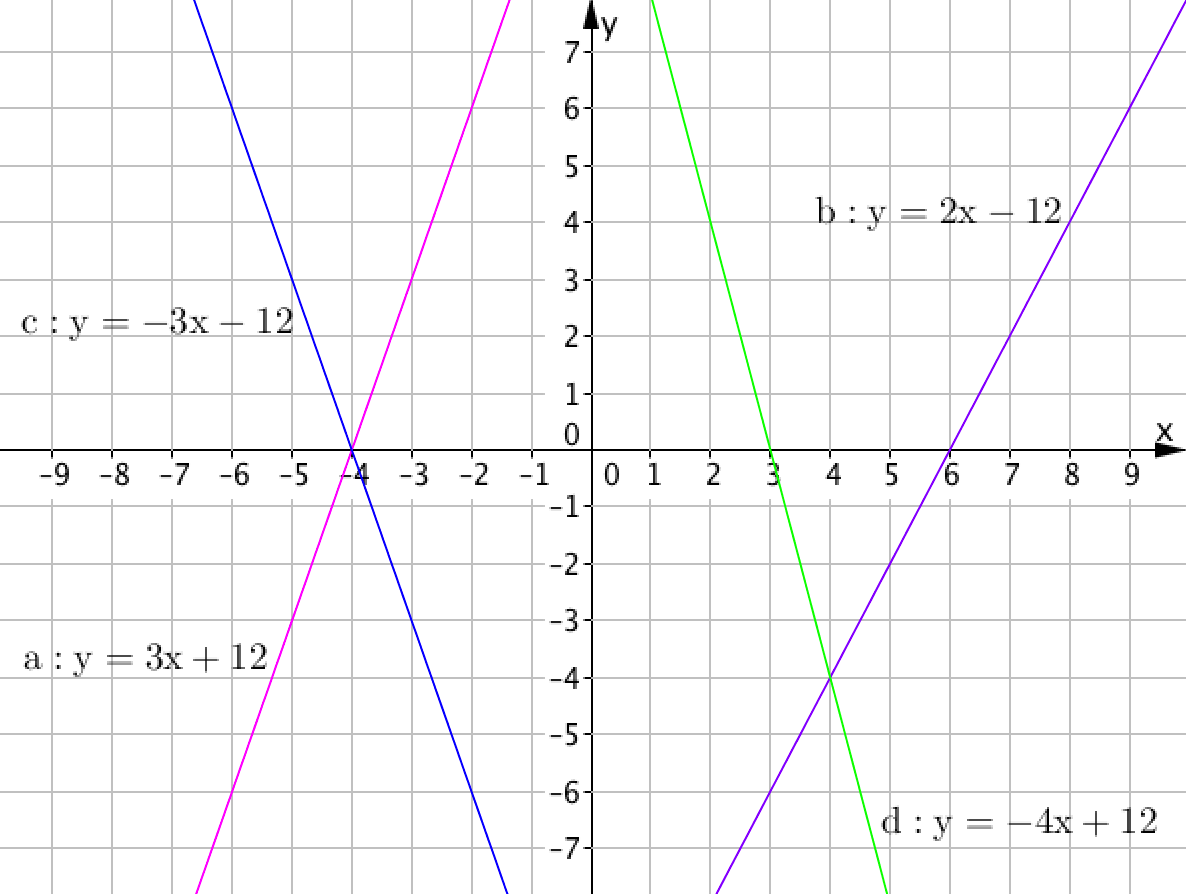
Нам необходимо выбрать прямую, которая дает линейное уравнение \(\displaystyle -4x+12=0\) при пересечении оси \(\displaystyle OX.\)
Найдем линейные уравнения, которые дает каждая прямая при пересечении с осью \(\displaystyle OX.\) Для этого будем заменять \(\displaystyle y\) на \(\displaystyle 0\) в каждом уравнении прямой:
- прямая \(\displaystyle a:\, \color{blue}{y}=3x+12 \) дает линейное уравнение \(\displaystyle \color{blue}{0}=3x+12,\)
- прямая \(\displaystyle b:\, \color{blue}{y}=2x-12 \) дает линейное уравнение \(\displaystyle \color{blue}{0}=2x-12,\)
- прямая \(\displaystyle c:\, \color{blue}{y}=-3x-12 \) дает линейное уравнение \(\displaystyle \color{blue}{0}=-3x-12,\)
- прямая \(\displaystyle d:\, \color{blue}{y}=-4x+12 \) дает линейное уравнение \(\displaystyle \color{blue}{0}=-4x+12.\)
Из полученных соответствий следует, что прямая \(\displaystyle d:\, y={\bf -4x+12} \) дает заданное линейное уравнение \(\displaystyle {\bf -4x+12}=0.\)
Ответ: прямая \(\displaystyle d.\)
Алгоритм получения прямой по заданному линейному уравнению
Прямая \(\displaystyle y={\bf ax+b}\) при пересечении с осью \(\displaystyle OX\) даёт линейное уравнение \(\displaystyle {\bf ax+b}=0.\)
Значит, можно сказать, что по линейному уравнению \(\displaystyle {\bf ax+b}=0\) можно построить прямую \(\displaystyle y={\bf ax+b}, \) которая дает заданное линейное уравнение.
В нашем случае по линейному уравнению \(\displaystyle -4x+12=0\) мы строим прямую \(\displaystyle d: y=-4x+12.\)