Төмендегі сызықтық теңдеу
\(\displaystyle 0,32(x+\frac{9}{25})+\frac{3}{100}x=0,1152+0,35x\)
және
\(\displaystyle y=0,32(x+\frac{9}{25})+\frac{3}{100}x-0,1152-0,35x{\small }\) сызықтық функцияның графигі берілген.
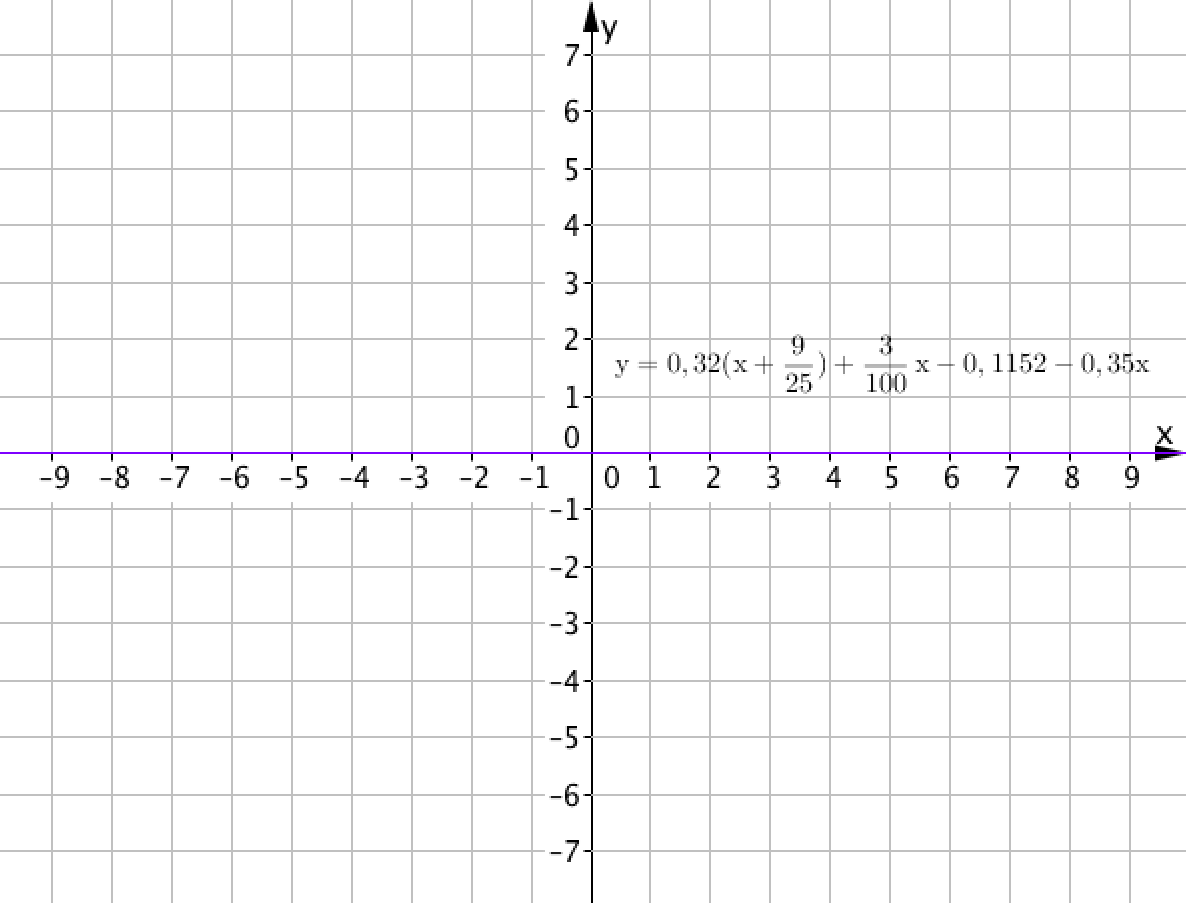
Берілген сызықтық теңдеудің шешімдерінің санын анықтаңыз
\(\displaystyle y=0,32(x+\frac{9}{25})+\frac{3}{100}x-0,1152-0,35x\)
түзуінің \(\displaystyle OX\) осімен қиылысу нүктесінің бірінші координаты (абсцисса) келесі сызықтық теңдеудің шешімі болып табылады
\(\displaystyle 0,32(x+\frac{9}{25})+\frac{3}{100}x-0,1152-0,35x=0{\small ,}\)
немесе, егер \(\displaystyle -0,1152-0,35x\) қарама-қарсы таңбамен оңға көшірілсе,
\(\displaystyle 0,32(x+\frac{9}{25})+\frac{3}{100}x=0,1152+0,35x{\small .}\)
Сондықтан төмендегі түзудің
\(\displaystyle y=0,32(x+\frac{9}{25})+\frac{3}{100}x-0,1152-0,35x\)
\(\displaystyle OX\) осімен қиылысу нүктелерінің саны сызықтық теңдеудің шешімдерінің санына сәйкес келеді
\(\displaystyle 0,32(x+\frac{9}{25})+\frac{3}{100}x=0,1152+0,35x{\small .}\)
Бірақ графиктен бізге берілген түзудің \(\displaystyle OX{\small .}\) осіне сәйкес келетінін көруге болады . Сондықтан сызықтық теңдеудің шешімдері барлық сандар болып табылады.
Жауабы: барлық сандар шешімдер болып табылады.