Төмендегі сызықтық теңдеу
\(\displaystyle \frac{7}{16}x-\frac{3}{25}=0,21875(2x+9)\)
және
\(\displaystyle y=\frac{7}{16}x-\frac{3}{25}-0,21875(2x+9){\small }\) сызықтық функцияның графигі берілген.
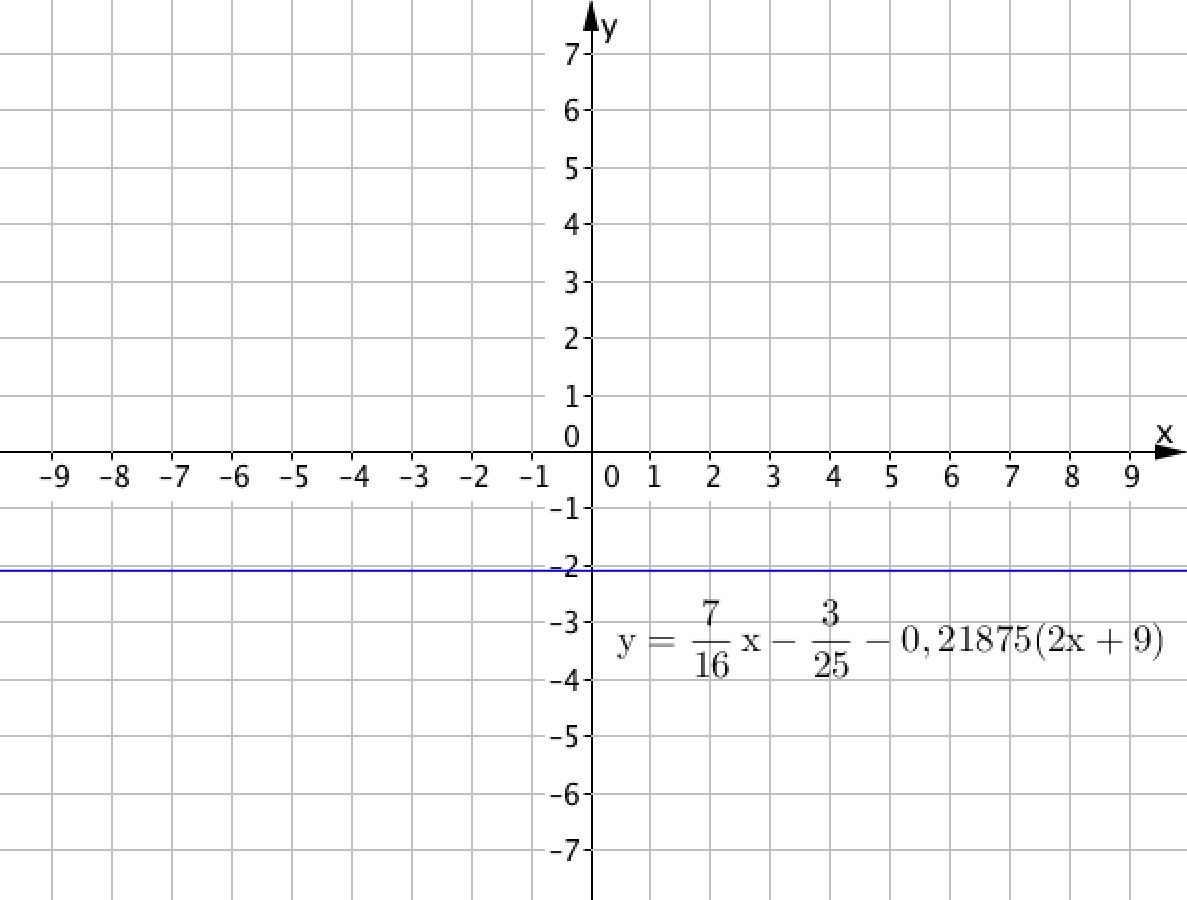
Берілген сызықтық теңдеудің шешімдерінің санын анықтаңыз.
\(\displaystyle y=\frac{7}{16}x-\frac{3}{25}-0,21875(2x+9)\) түзуінің \(\displaystyle OX\) осімен қиылысу нүктесінің бірінші координаты (абсцисса) келесі сызықтық теңдеудің шешімі болып табылады
\(\displaystyle \frac{7}{16}x-\frac{3}{25}-0,21875(2x+9)=0{\small ,}\)
немесе, егер \(\displaystyle -0,21875(2x+9)\) қарама-қарсы таңбамен оңға көшірілсе,
\(\displaystyle \frac{7}{16}x-\frac{3}{25}=0,21875(2x+9){\small .}\)
Сондықтан төмендегі түзудің
\(\displaystyle y=\frac{7}{16}x-\frac{3}{25}-0,21875(2x+9)\)
\(\displaystyle OX\) осімен қиылысу нүктелерінің саны сызықтық теңдеудің шешімдерінің санына сәйкес келеді
\(\displaystyle \frac{7}{16}x-\frac{3}{25}=0,21875(2x+9){\small .}\)
Графиктен түзудің \(\displaystyle OX\) осіне параллель екенін, сондықтан оны бірде-бір нүктеде қиып өтпейтінін көруге болады. Бұл сызықтық теңдеудің шешімдері жоқ дегенді білдіреді.
Жауабы: шешімдері жоқ.