Есептеулерге жүгінбестен,
\(\displaystyle 2x+\frac{6x-5}{7}-\frac{8x+7}{3}=0\) сызықтық теңдеуін шешіңіз,
егер
\(\displaystyle y=2x+\frac{6x-5}{7}-\frac{8x+7}{3}\) сызықтық функциясының графигі белгілі болса.
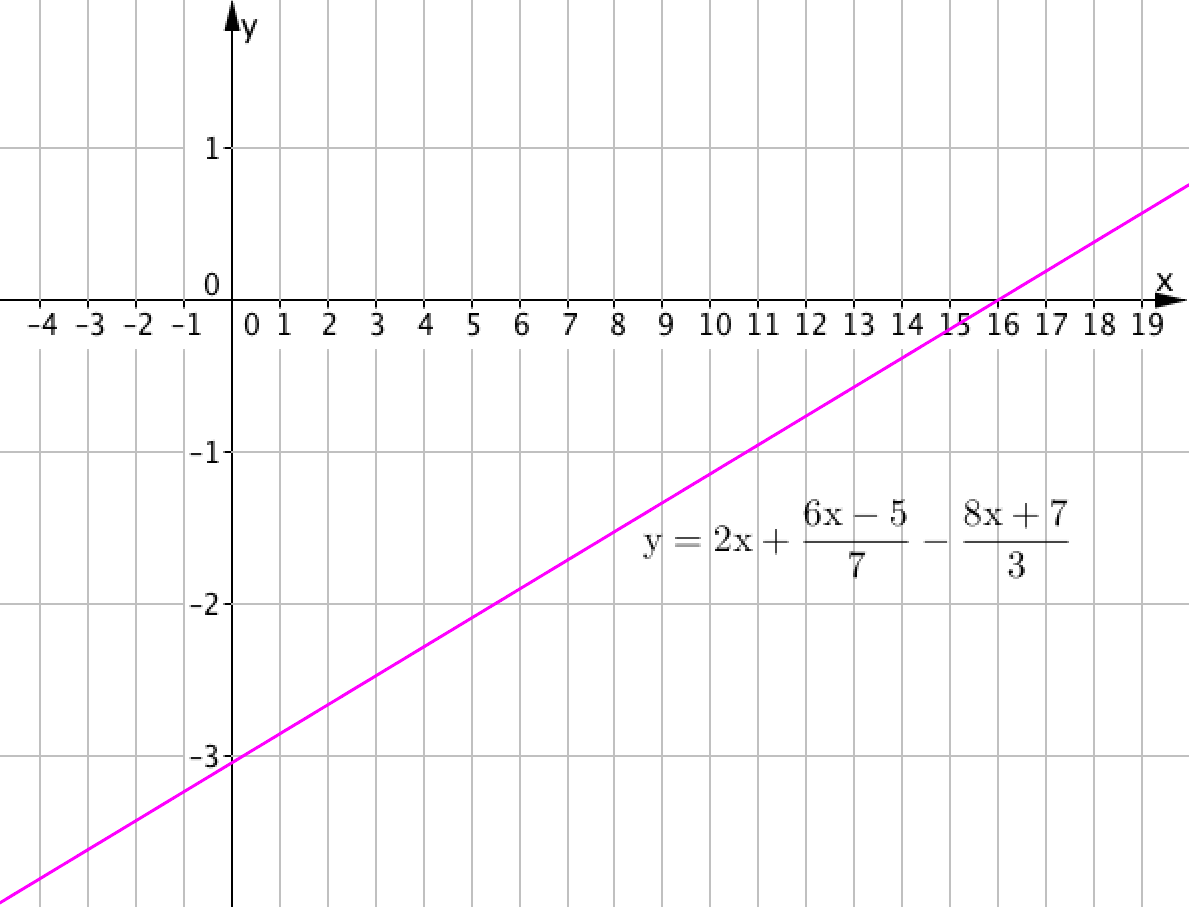
\(\displaystyle x=\)
\(\displaystyle y=2x+\frac{6x-5}{7}-\frac{8x+7}{3}\) түзуінің \(\displaystyle OX\) осімен қиылысу нүктесі (абсцисса осі) \(\displaystyle (x_{0};0),\)координатасына ие, мұндағы \(\displaystyle x_{0}\) - \(\displaystyle 2x+\frac{6x-5}{7}-\frac{8x+7}{3}=0\) сызықтық теңдеуінің шешімі.
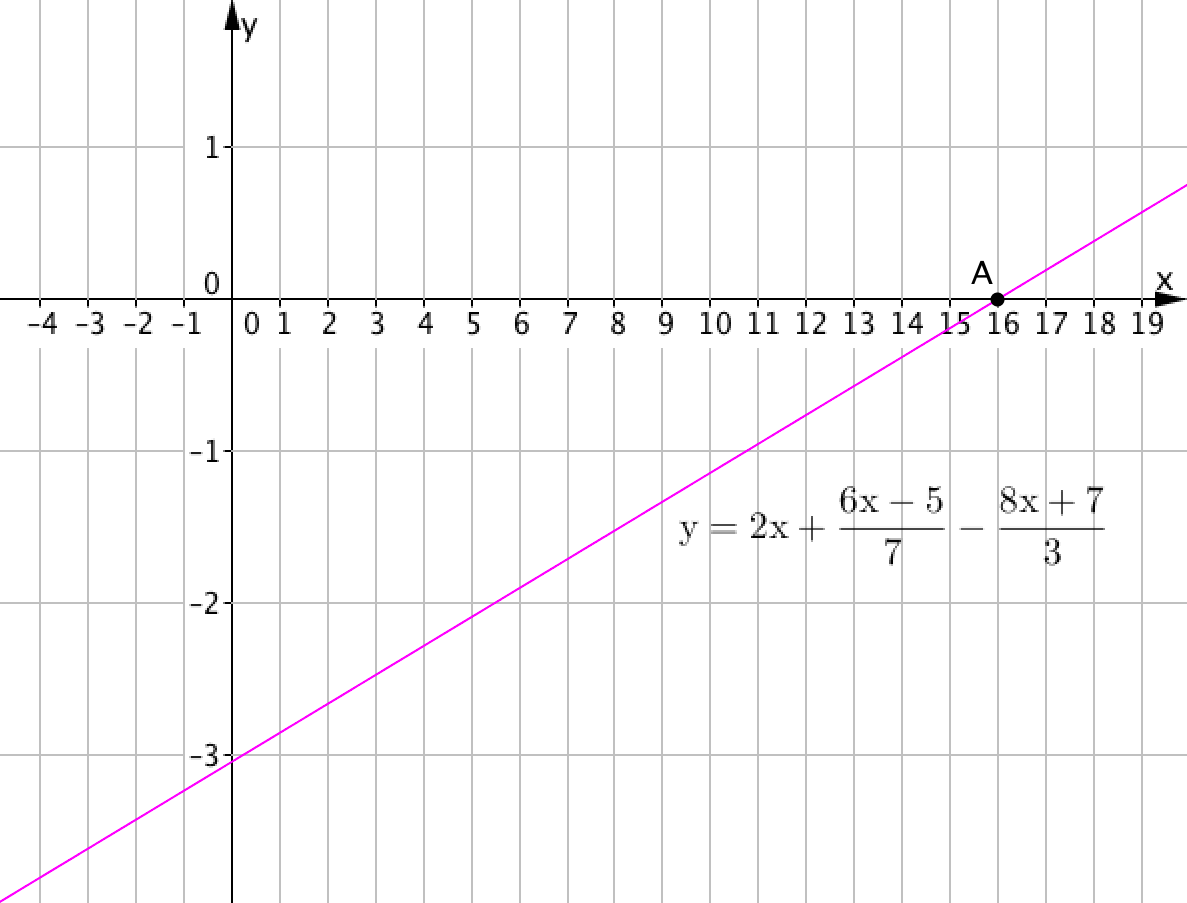
Суреттен \(\displaystyle y=2x+\frac{6x-5}{7}-\frac{8x+7}{3}\) сызықтық функциясының графигі \(\displaystyle OX\) осін \(\displaystyle x=16\) абсциссасымен \(\displaystyle A\,(16;0)\) нүктесінде қиып өтетінін көруге болады.
Сондықтан \(\displaystyle x=16\) \(\displaystyle 2x+\frac{6x-5}{7}-\frac{8x+7}{3}=0\) сызықтық теңдеуінің түбірі болып табылады.
Жауабы: \(\displaystyle x=16.\)