Сәйкес сызықтық теңдеуді шешу арқылы
\(\displaystyle y=\frac{3}{5}x+\frac{1}{7}\)
түзуінің \(\displaystyle OX\) осімен қиылысуындағы \(\displaystyle A\) нүктесінің координаттарын табыңыз:
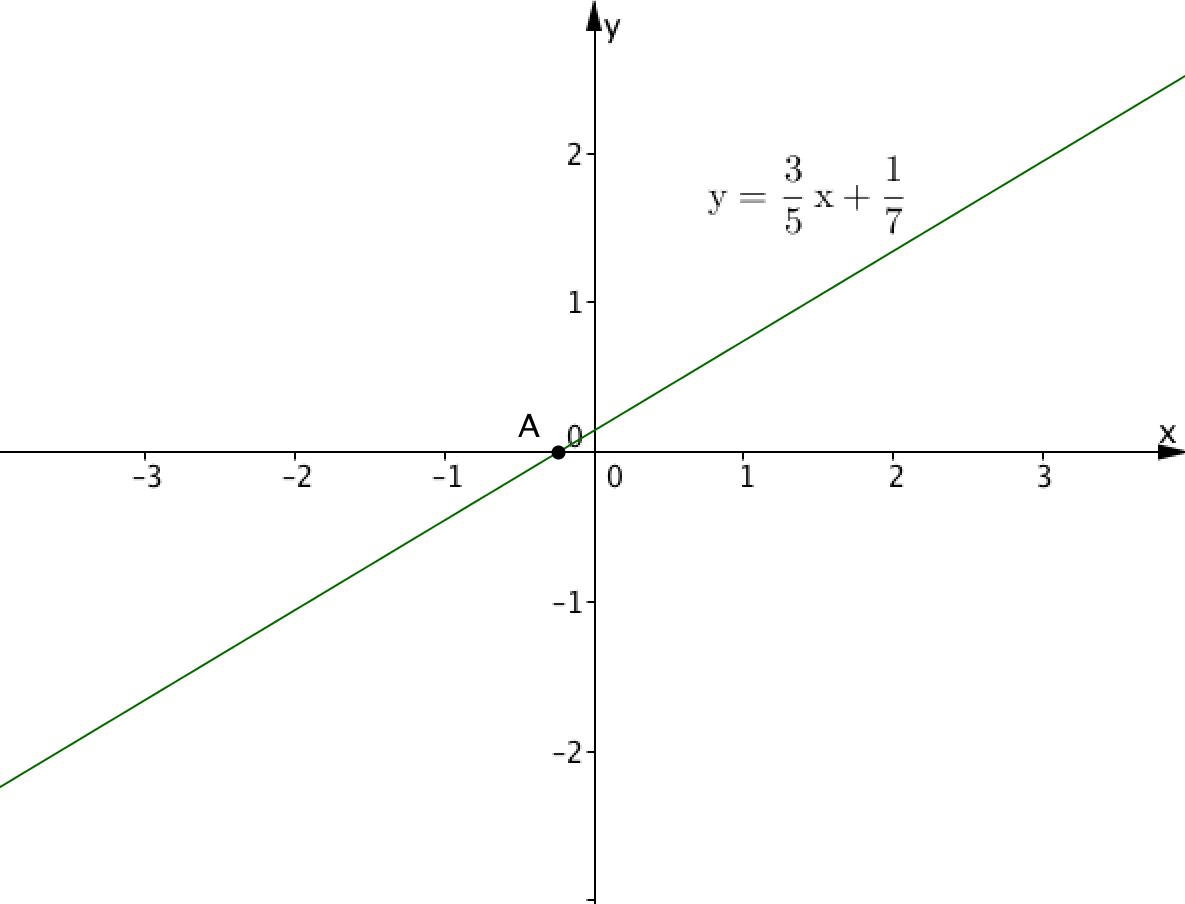
\(\displaystyle A(x_{0};y_{0})\) нүктесі \(\displaystyle y=\frac{3}{5}x+\frac{1}{7}\) сызығының \(\displaystyle OX\) осімен қиылысу нүктесі болып табылады.
Сондықтан:
- \(\displaystyle y_{0}=0\) координатасы,
- \(\displaystyle x_{0}\) координатасы \(\displaystyle \frac{3}{5}x+\frac{1}{7}=0\) сызықтық теңдеуінің шешімі болып табылады,
ол \(\displaystyle y=\frac{3}{5}x+\frac{1}{7}\) түзуінің \(\displaystyle OX\) осімен қиылысуынан алынады.
Сызықтық теңдеуді шешейік:
\(\displaystyle \frac{3}{5}x+\frac{1}{7}=0.\)
\(\displaystyle \frac{1}{7}\) теңдеудің оң жағына қарама қарсы таңбамен көшірейік:
\(\displaystyle \frac{3}{5}x=-\frac{1}{7}.\)
Теңдеудің екі бөлігін де \(\displaystyle \frac{3}{5}\) бөлейік:
\(\displaystyle \frac{3}{5}x:\frac{3}{5}=\left(-\frac{1}{7}\right):\frac{3}{5},\)
\(\displaystyle x=\left(-\frac{1}{7}\right)\cdot \frac{5}{3},\)
\(\displaystyle x=-\frac{5}{21}.\)
Осылайша,
\(\displaystyle x_{0}=-\frac{5}{21}\) координатасы,
ал \(\displaystyle A\) нүктесі
\(\displaystyle \left(-\frac{5}{21};0 \right)\) координаттарына ие
Жауабы: \(\displaystyle \left(-\frac{5}{21};0 \right).\)