Уравнение \(\displaystyle \cos(2x)+\sin^2(x)=0{,}75\) равносильно двум уравнениям:
\(\displaystyle \sin(x)=\frac{1}{2}\) или \(\displaystyle \sin(x)=-\frac{1}{2}{\small .}\)
Уравнение \(\displaystyle \sin(x)=-\frac{1}{2}\) имеет решения:
\(\displaystyle x_1=\frac{7\pi}{6}+2\pi n, \, n\in \mathbb{Z}\) и \(\displaystyle x_2=\frac{11\pi}{6}+2\pi n, \, n\in \mathbb{Z}{ \small .}\)
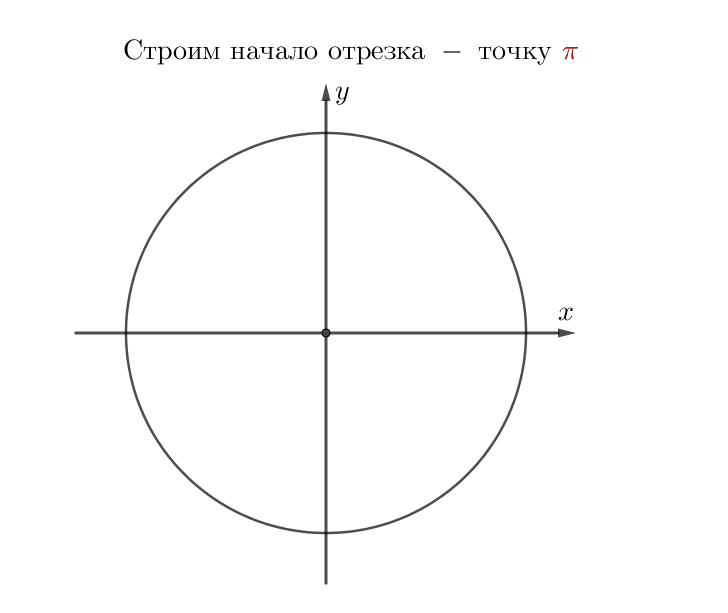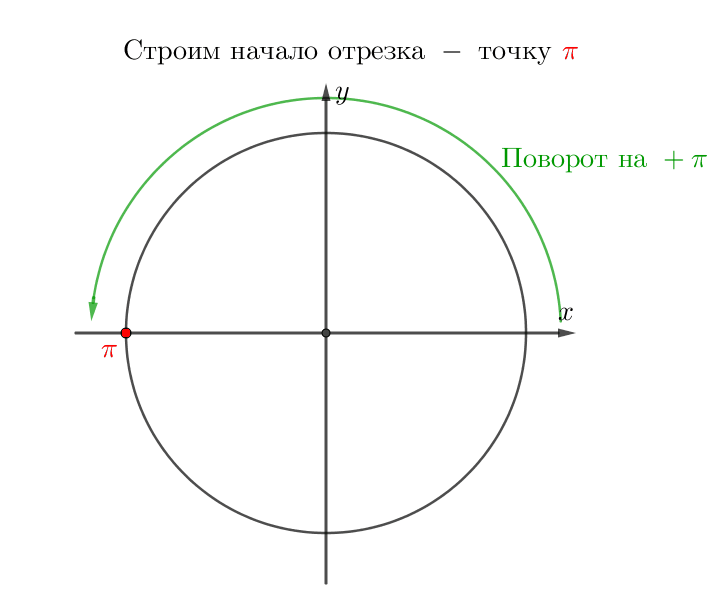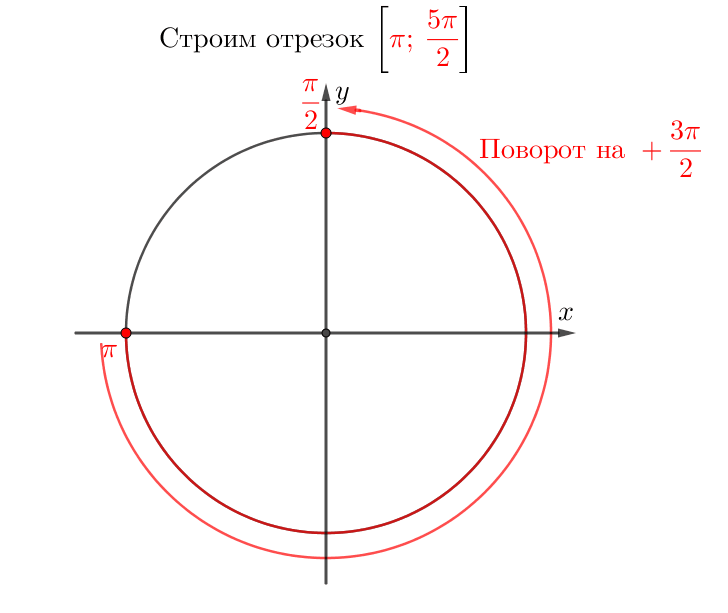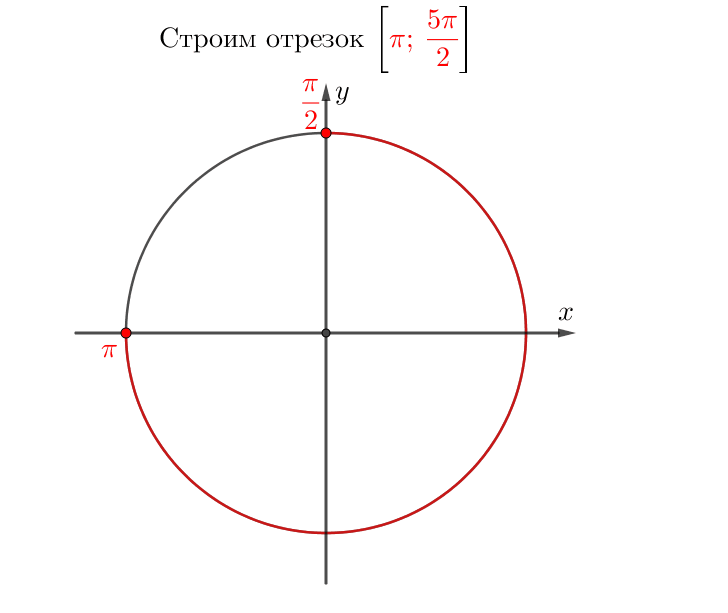
Выберите корни уравнения \(\displaystyle \sin(x)=-\frac{1}{2}\) из промежутка \(\displaystyle \left[\pi;\, \frac{5\pi}{2}\right]{\small.}\)
\(\displaystyle x_1=\frac{7\pi}{6}{\small,}\)
\(\displaystyle x_2=\frac{11\pi}{6}{\small.}\)
Выберем корни из отрезка \(\displaystyle \left[\pi;\, \frac{5\pi}{2}\right]{\small .}\)
Таким образом, уравнение \(\displaystyle \sin(x)=-\frac{1 }{2}\) на отрезке \(\displaystyle \left[\pi;\, \frac{5\pi}{2}\right]\) имеет решения \(\displaystyle \frac{7\pi}{6}\) и \(\displaystyle \frac{11\pi}{6}{\small .}\)
Ответ: \(\displaystyle \frac{7\pi}{6}\) и \(\displaystyle \frac{11\pi}{6}{\small .}\)