Выберите график функции \(\displaystyle y=0{,}3(x-1)^2+2{\small .}\)
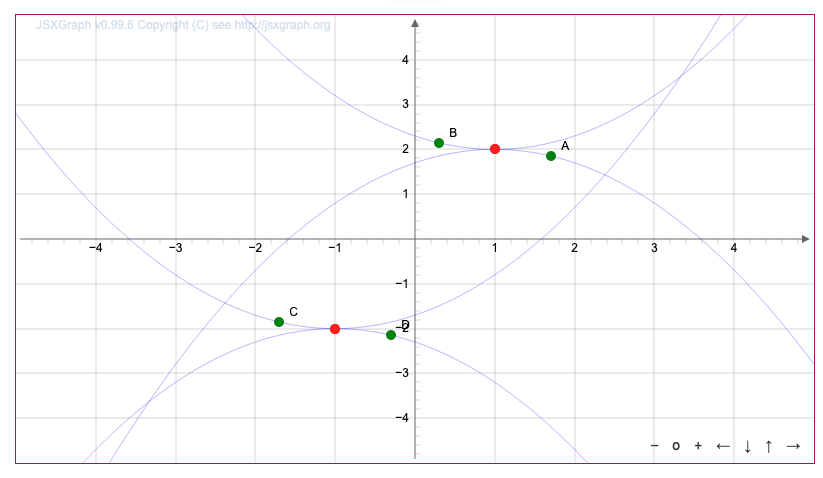
У каждой из данных парабол известна вершина:
парабола \(\displaystyle \rm A\) имеет вершину в точке \(\displaystyle (1;2){\small ,}\)
парабола \(\displaystyle \rm В\) имеет вершину в точке \(\displaystyle (1;2){\small ,}\)
парабола \(\displaystyle \rm D\) имеет вершину в точке \(\displaystyle (-1;-2){\small ,}\)
парабола \(\displaystyle \rm C\) имеет вершину в точке \(\displaystyle (-1;-2){\small .}\)
Согласно определению
Вершина параболы, заданной уравнением \(\displaystyle y=k(x-a)^2+b\)
Вершиной параболы, заданной уравнением \(\displaystyle y=k(x-a)^2+b{ \small ,}\) называется точка с координатами \(\displaystyle (a;\,b){\small.}\)
парабола, заданная уравнением \(\displaystyle y=0{,}3(x-1)^2+2{ \small ,}\) имеет вершину в точке \(\displaystyle (1;2){\small .}\)
Это соответствует графикам \(\displaystyle \rm A\) и \(\displaystyle \rm B{\small .}\)
Так как коэффициент \(\displaystyle k=0{,}3>0{\small ,}\) то ветви у искомой параболы должны быть направлены вверх.
Ветви параболы \(\displaystyle \rm A\) направлены вниз.
Ветви параболы \(\displaystyle \rm В\) направлены вверх.
Таким образом, уравнению \(\displaystyle y=0{,}3(x-1)^2+2\) соответствует график \(\displaystyle \rm В{\small .}\)
Ответ:\(\displaystyle \rm В{\small .}\)