Перемещая вершину \(\displaystyle O\) параболы \(\displaystyle y=3x^2{ \small ,}\) постройте график функции \(\displaystyle y=3(x-1)^2+1{\small .}\)
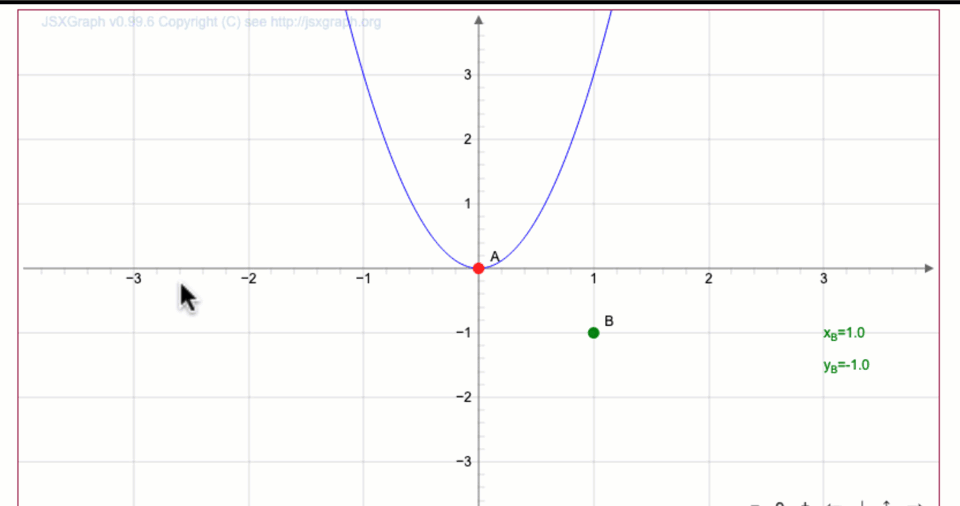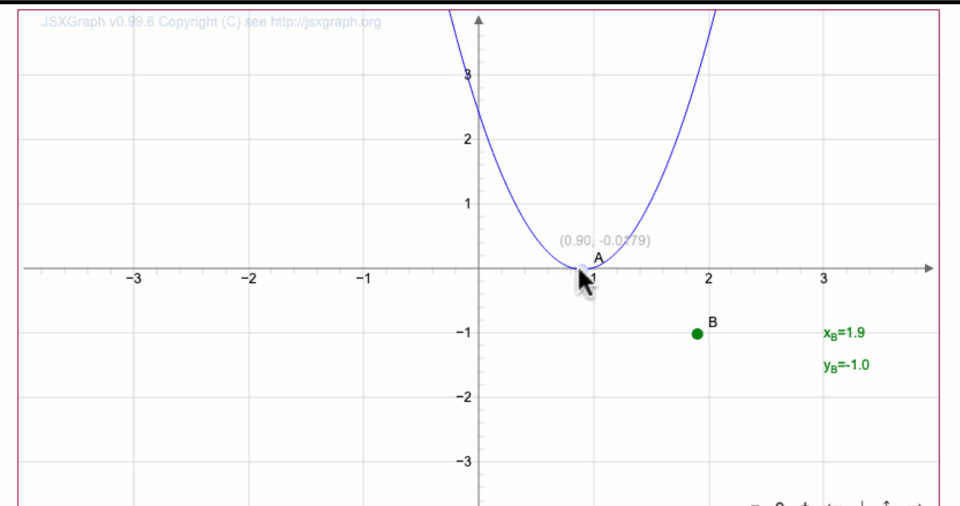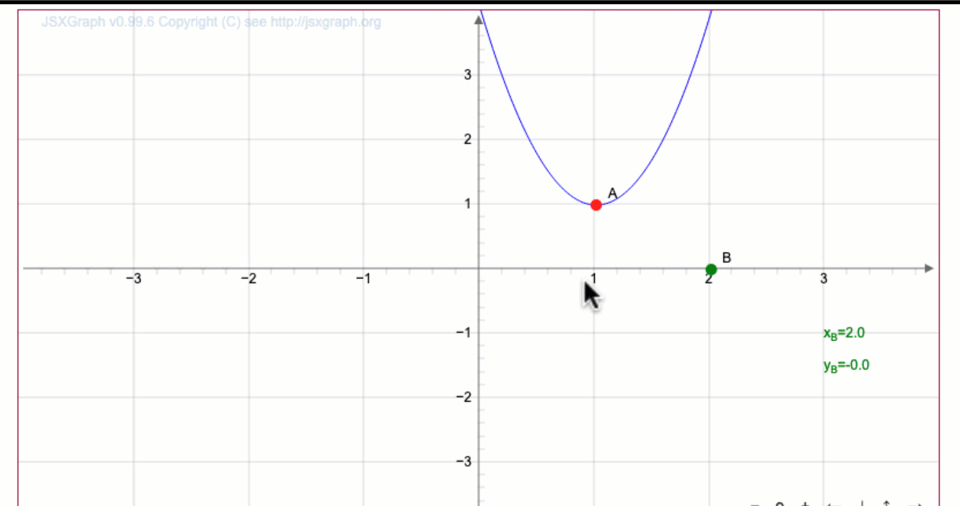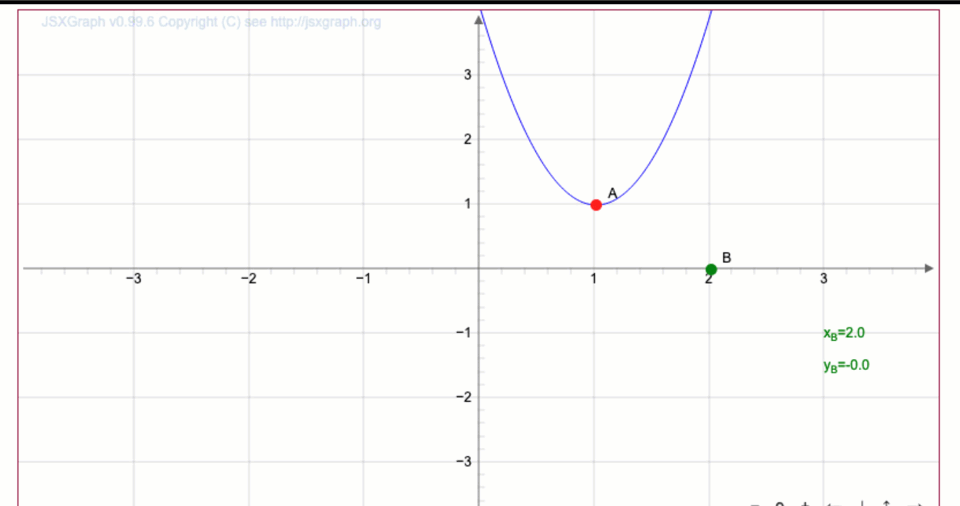
Запишите координаты точки \(\displaystyle \color{green}{В}\) на полученной кривой
\(\displaystyle \color{green}{В}=(\)\(\displaystyle \, ;\)\(\displaystyle )\)
с точностью до десятых
График функции \(\displaystyle y=k(x-a)^2+b\) получен из графика параболы \(\displaystyle y=kx^2\)
- сдвигом каждой точки на \(\displaystyle a\) единиц вправо вдоль оси \(\displaystyle \rm OX{\small ,}\)
- сдвигом каждой точки на \(\displaystyle b\) единиц вверх вдоль оси \(\displaystyle \rm OY{\small .}\)
Тогда вершина параболы \(\displaystyle y=kx^2\) точка \(\displaystyle (0;\,0)\) перейдёт в точку \(\displaystyle (0+a;0+b)=(a;\,b){\small .}\)
Вершина параболы, заданной уравнением \(\displaystyle y=k(x-a)^2+b\)
Вершиной параболы, заданной уравнением \(\displaystyle y=k(x-a)^2+b{ \small ,}\) называется точка с координатами \(\displaystyle (a;\,b){\small.}\)
Поэтому для построения графика функции \(\displaystyle y=3(x-1)^2+1\) требуется переместить вершину \(\displaystyle O\) параболы \(\displaystyle y=3x^2\) в вершину параболы \(\displaystyle y=3(x-1)^2+1{\small .}\)
Вершина параболы, заданной уравнением \(\displaystyle y=3(x-1)^2+1{ \small ,}\) имеет координаты \(\displaystyle (1;\,1){\small .}\)

Тогда точка \(\displaystyle B\) имеет координаты \(\displaystyle (2;\, -2){\small .}\)