Дан график функции \(\displaystyle y=x^2{\small .}\) Постройте график функции \(\displaystyle y=(x-1)^2+2\)
и найдите координаты точки
\(\displaystyle A=(\)\(\displaystyle ;\) \(\displaystyle )\)
с точностью до десятых.
Перемещайте график, изменяя параметры \(\displaystyle a\) и \(\displaystyle b\) ползунками с точностью до сотых.
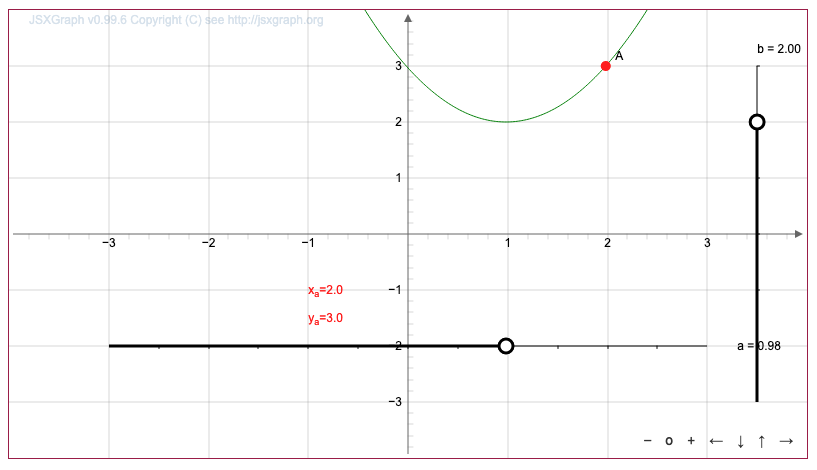
Требуется получить из параболы \(\displaystyle y=x^2\) график функции \(\displaystyle y=(x-1)^2+2{\small .}\)
- Если график функции \(\displaystyle y=f(x) \) сдвинуть на \(\displaystyle \color{blue}{\rm A} \) единиц вправо, получится график функции \(\displaystyle y=f(x{\bf-}\color{blue}{\rm A}){\small . } \)
- Если график функции \(\displaystyle y=f(x) \) сдвинуть на \(\displaystyle \color{blue}{\rm A} \) единиц влево, получится график функции \(\displaystyle y=f(x{\bf+}\color{blue}{\rm A}){\small . } \)
Получаем сдвиг на \(\displaystyle 1\) единицу вправо:
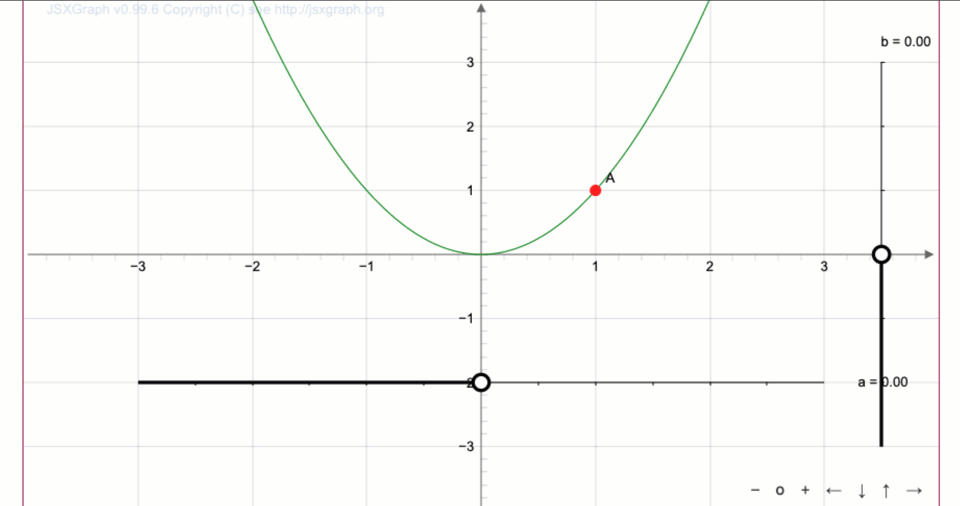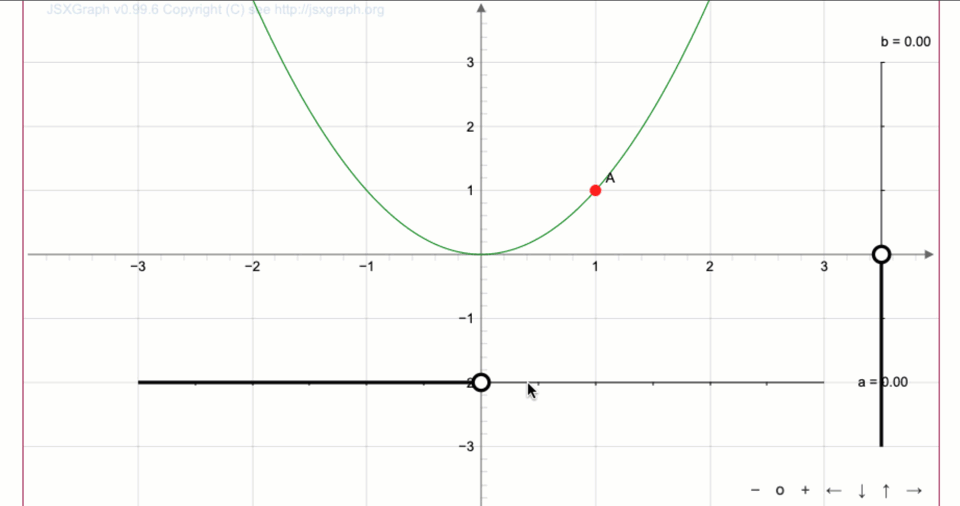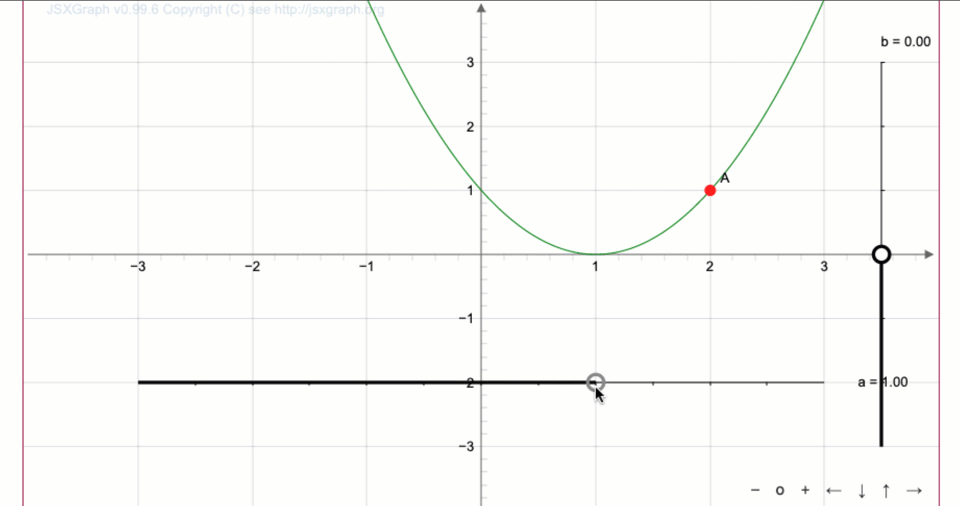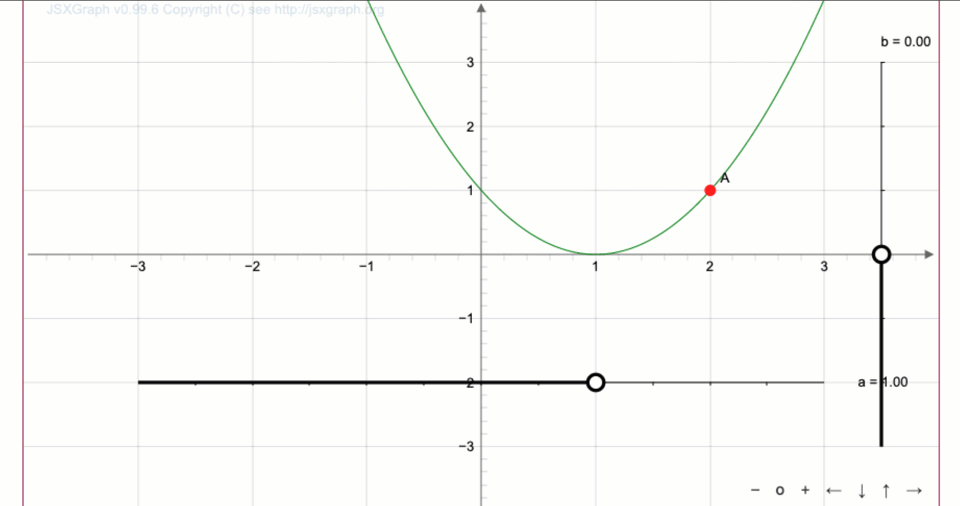
- Если график функции \(\displaystyle y=f(x) \) сдвинуть на \(\displaystyle \color{blue}{\rm A} \) единиц вверх, получится график функции \(\displaystyle y=f(x){\bf+}\color{blue}{\rm A}{\small . } \)
- Если график функции \(\displaystyle y=f(x) \) сдвинуть на \(\displaystyle \color{blue}{\rm A} \) единиц вниз, получится график функции \(\displaystyle y=f(x){\bf-}\color{blue}{\rm A}{\small . } \)
Получаем сдвиг на \(\displaystyle 2\) единицы вверх:
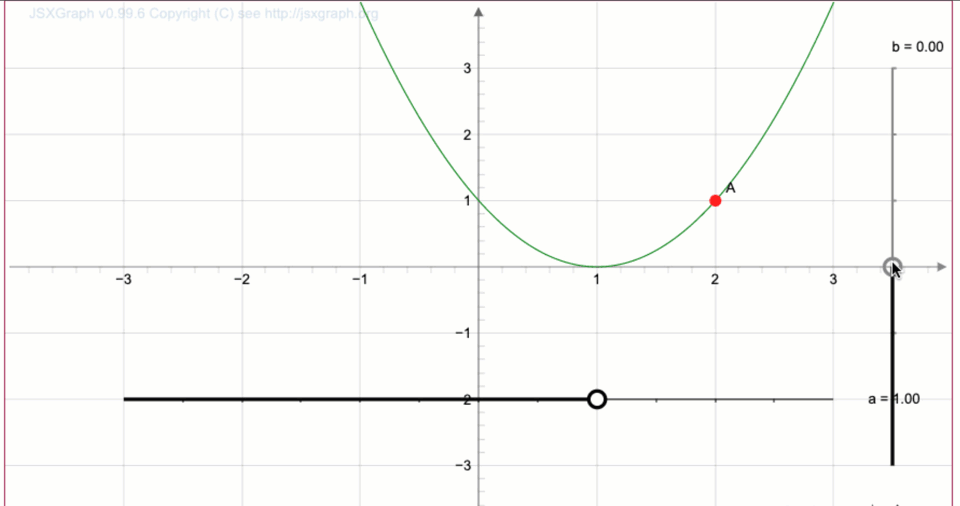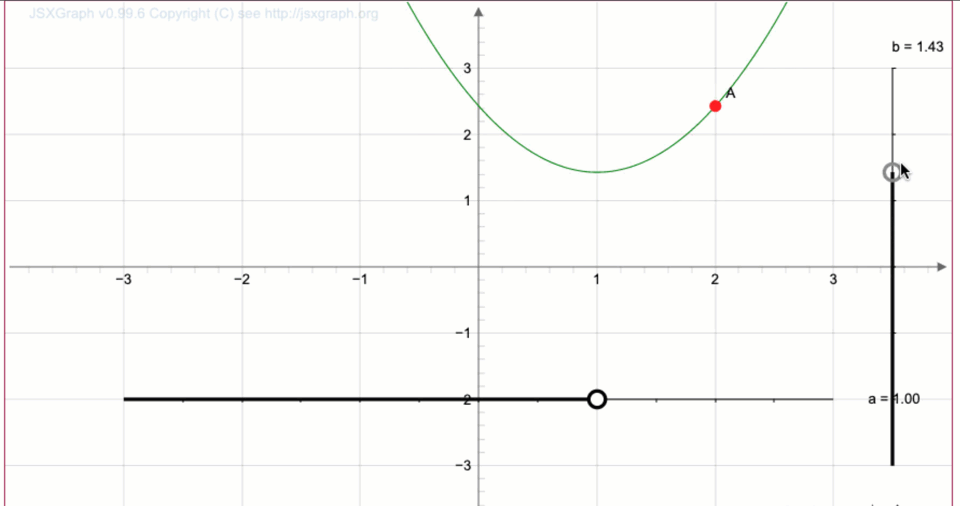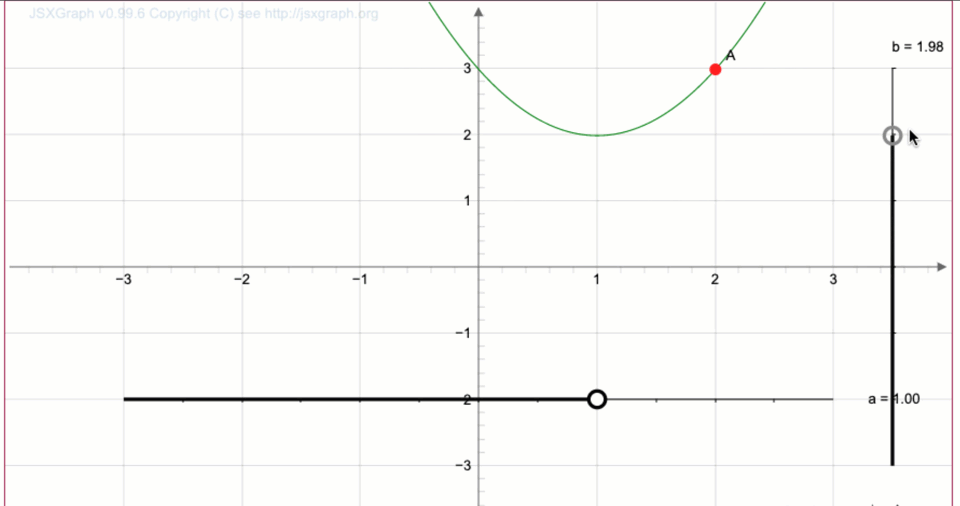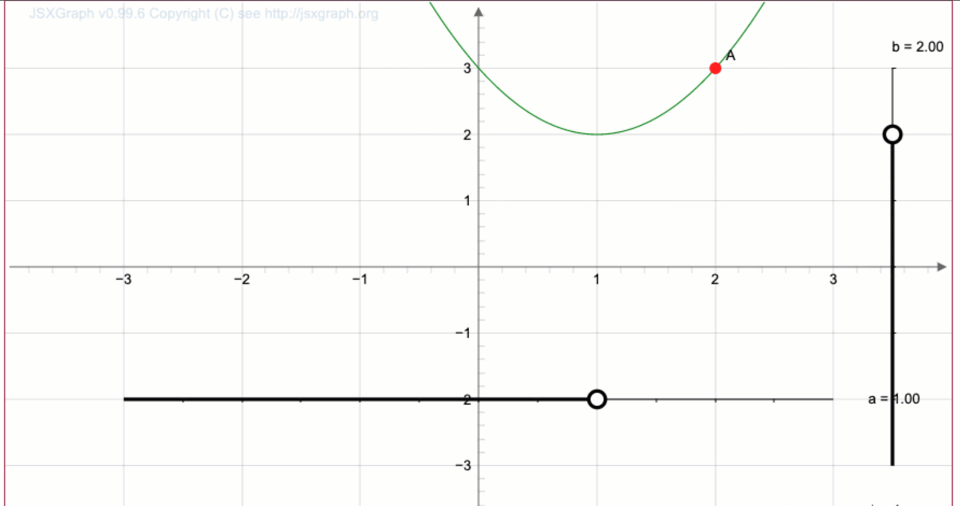
Наводя указатель мыши на точку, получаем координаты

После округления до десятых получаем координаты \(\displaystyle (2;\,3){\small .}\)
Ответ: \(\displaystyle A=(2;\,3){\small .}\)