В прямоугольном треугольнике \(\displaystyle ABC\) угол \(\displaystyle C\) прямой, \(\displaystyle \angle B=58^{\circ},\) \(\displaystyle CD-\)медиана. Найдите \(\displaystyle \angle ACD{\small .}\)
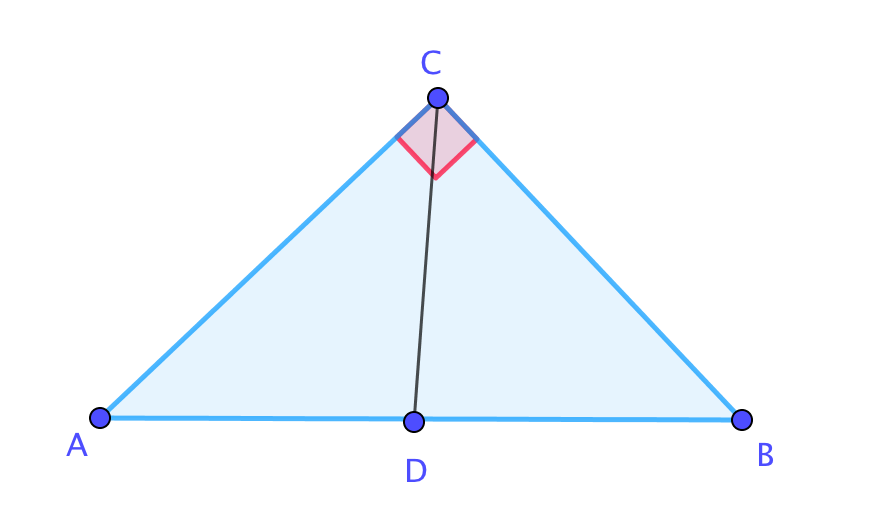
Медиана, проведенная к гипотенузе, равна половине гипотенузы, то есть \(\displaystyle AD=CD=BD{\small . } \) Получаем, что треугольники \(\displaystyle CDB \) и \(\displaystyle ACD \) равнобедренные.
Значит,
\(\displaystyle \angle DCB= \angle CBD= 58^\circ{\small ,}\)
\(\displaystyle \angle ACD= \angle CAD{\small . } \)
Угол \(\displaystyle C \) равен \(\displaystyle 90^\circ \) и равен \(\displaystyle \angle ACD+ \angle DCB{\small . }\) Поэтому
\(\displaystyle 90^\circ= \angle ACD+ \angle DCB{\small , } \)
\(\displaystyle 90^\circ= \angle ACD+ 58^\circ{\small , } \)
\(\displaystyle \angle ACD= 90^\circ- 58^\circ{\small , } \)
\(\displaystyle \angle ACD= 32^\circ{\small . } \)
Значит,
\(\displaystyle \angle A= \angle CAD= \angle ACD= 32^\circ{\small .} \)
Ответ: \(\displaystyle 32 {\small .} \)