В треугольнике \(\displaystyle ABC\) стороны \(\displaystyle AC\) и \(\displaystyle BC\) равны. Внешний угол при вершине \(\displaystyle B\) равен \(\displaystyle 138^{\circ}{\small .}\)
Найдите угол \(\displaystyle \angle C{\small .}\)
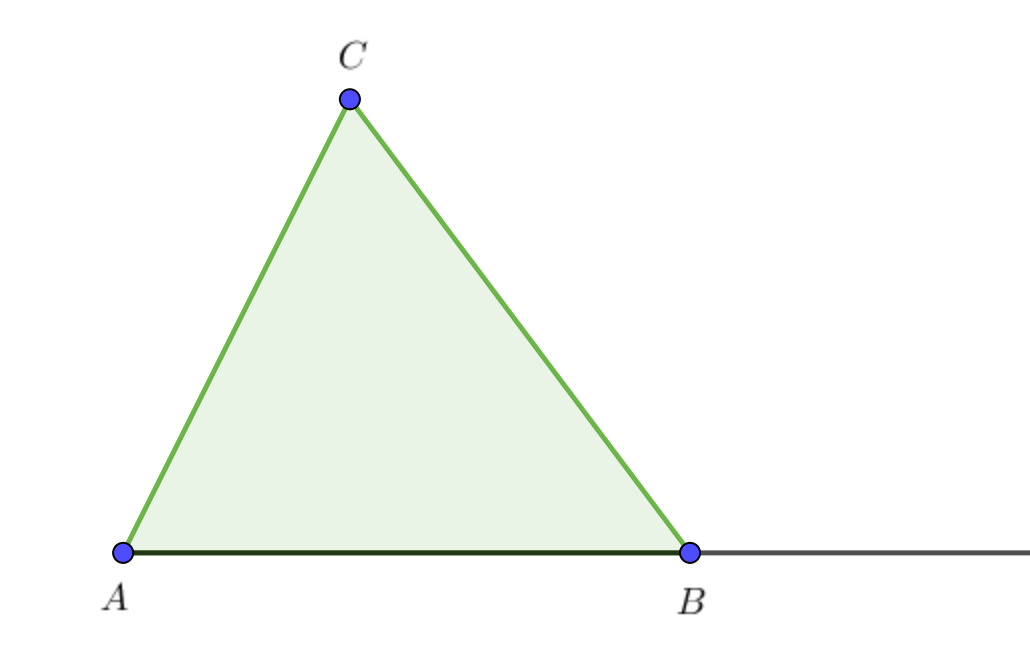
Внешний угол при вершине \(\displaystyle C \) равен сумме двух внутренних углов, несмежных с ним:
\(\displaystyle \angle A+ \angle C= 138^\circ{\small . } \)
В равнобедренном треугольнике углы при основании равны. В нашем случае \(\displaystyle \angle A= \angle B{\small . } \) Из того, что
\(\displaystyle \angle A+ \angle B+ \angle C=180^\circ{\small , } \)
\(\displaystyle \angle A+ \angle A+ \angle C=180^\circ{\small , } \)
получаем
\(\displaystyle 2\angle A+ \angle C=180^\circ{\small . } \)
Тогда имеем систему:
\(\displaystyle \left\{\begin{aligned}2\angle A+ \angle C&=180^\circ{\small , }\\\angle A+ \angle C&= 138^\circ{\small .}\end{aligned}\right. \)
Из первого уравнения \(\displaystyle \angle C= 180^\circ- 2\angle A{\small . } \) Подставляя во второе, получаем:
\(\displaystyle \angle A+ 180^\circ- 2\angle A= 138^\circ{\small , } \)
\(\displaystyle -\angle A= 138^\circ- 180^\circ{\small , } \)
\(\displaystyle -\angle A= -42^\circ{\small , } \)
\(\displaystyle \angle A= 42^\circ{\small . } \)
Таким образом,
\(\displaystyle \angle C= 180^\circ- 2\angle A{\small , } \)
\(\displaystyle \angle C= 180^\circ- 2\cdot 42^\circ{\small , } \)
\(\displaystyle \angle C= 180^\circ- 84^\circ{\small , } \)
\(\displaystyle \angle C= 96^\circ {\small.}\)
Ответ: \(\displaystyle 96 {\small . } \)