В треугольнике \(\displaystyle ABC\) угол \(\displaystyle \angle C=50^{\circ}{\small , }\) \(\displaystyle AD\) биссектриса, \(\displaystyle \angle CAD=28^{\circ}{\small .}\) Найдите угол \(\displaystyle B{\small .}\)
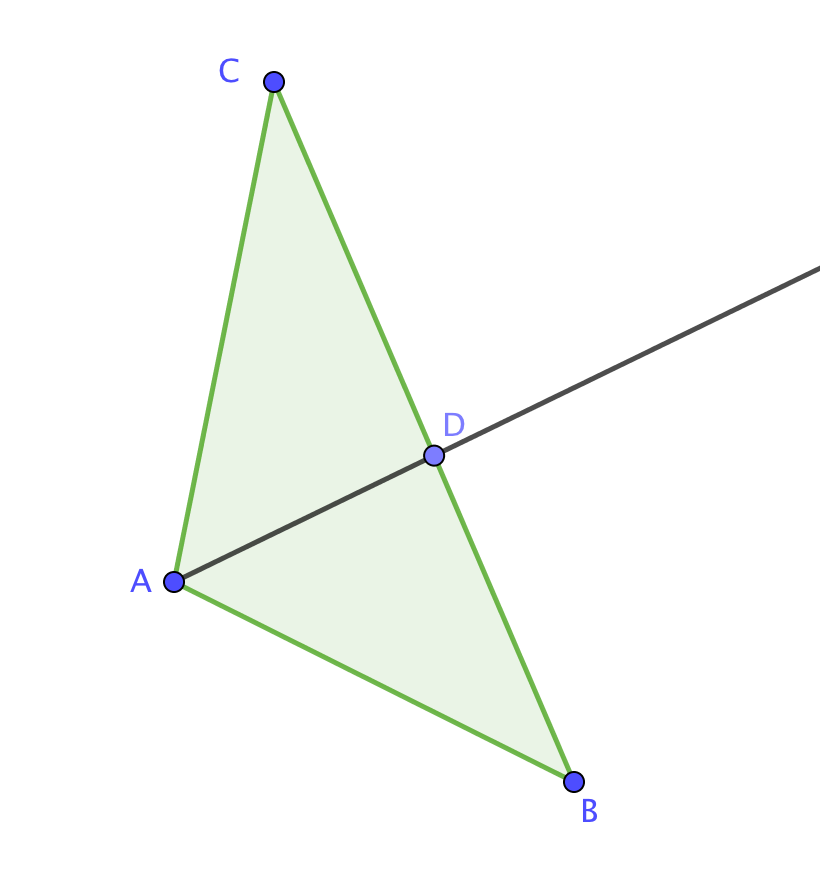
Так как \(\displaystyle AD \) – биссектриса угла \(\displaystyle A{\small , } \) то \(\displaystyle \angle BAD= \angle CAD=28^\circ{\small . } \)
Значит, \(\displaystyle \angle A= \angle BAD+\angle CAD= 28^\circ+ 28^\circ= 56^\circ{\small .} \)
Сумма углов в треугольнике равна \(\displaystyle 180^\circ{\small , } \) поэтому
\(\displaystyle \angle A+ \angle B+ \angle C=180^\circ{\small , } \)
\(\displaystyle 56^\circ+ \angle B+50^\circ= 180^\circ{\small , }\)
\(\displaystyle \angle B= 180^\circ- 50^\circ- 56^\circ {\small , }\)
\(\displaystyle \angle B= 74^\circ{\small . } \)
Ответ: \(\displaystyle 74 {\small . } \)