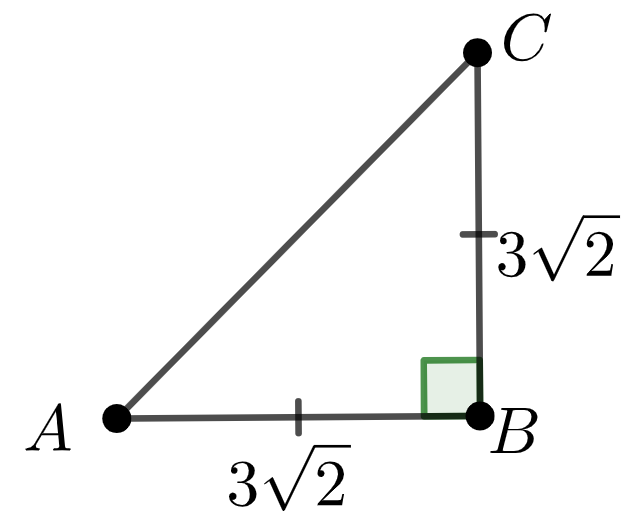
В правильной четырехугольной пирамиде сторона основания равна \(\displaystyle 3\sqrt{2}{\small ,}\) а объем равен \(\displaystyle 24{\small .}\) Найдите боковое ребро.
Правильная пирамида
Пирамида называется правильной, если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
Пусть \(\displaystyle ABCD\) – основание, \(\displaystyle SO\) – высота, \(\displaystyle S\) – вершина данной пирамиды.
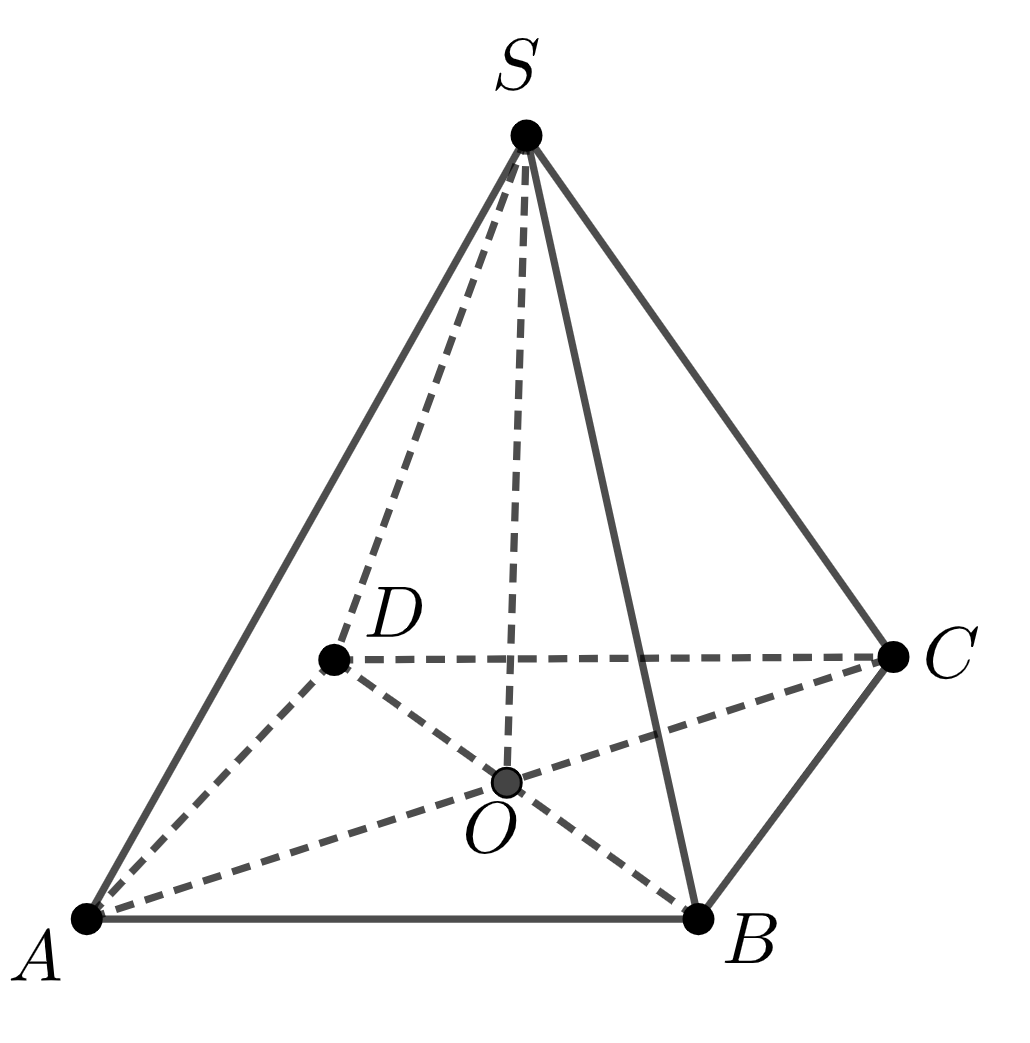
Перпендикулярность прямой и плоскости
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
\(\displaystyle SO\) – высота пирамиды \(\displaystyle SABCD\), значит, \(\displaystyle SO\) перпендикулярна плоскости основания, в которой лежит \(\displaystyle OC{\small .}\)
Следовательно, \(\displaystyle SO\perp АC{\small .}\)
Рассмотрим треугольник \(\displaystyle SАC{\small. }\)
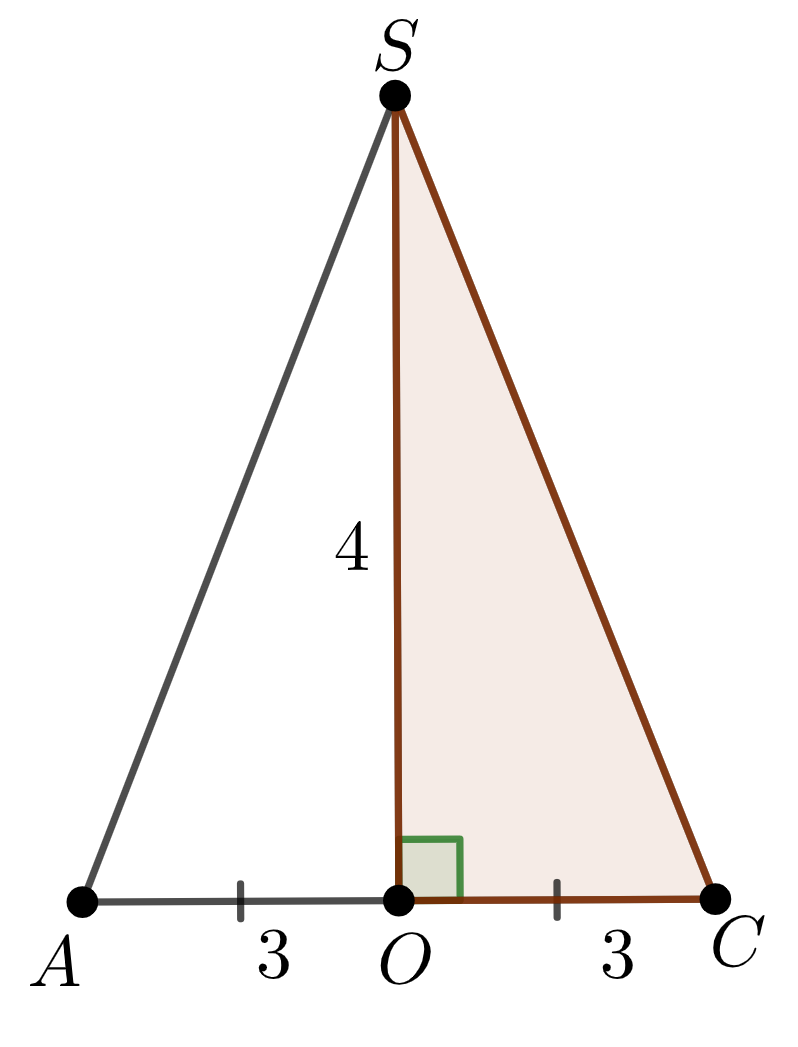
Найдем \(\displaystyle SC\) по теореме Пифагора для треугольника \(\displaystyle SOC{\small :}\)
\(\displaystyle SO^2+OC^2=SC^2{\small,}\)
\(\displaystyle 4^2+3^2=SC^2{\small ,}\)
\(\displaystyle SC^2=25{\small .}\)
Так как длина отрезка положительна, то
\(\displaystyle SC=5{\small .}\)
Ответ: \(\displaystyle 5{\small .}\)