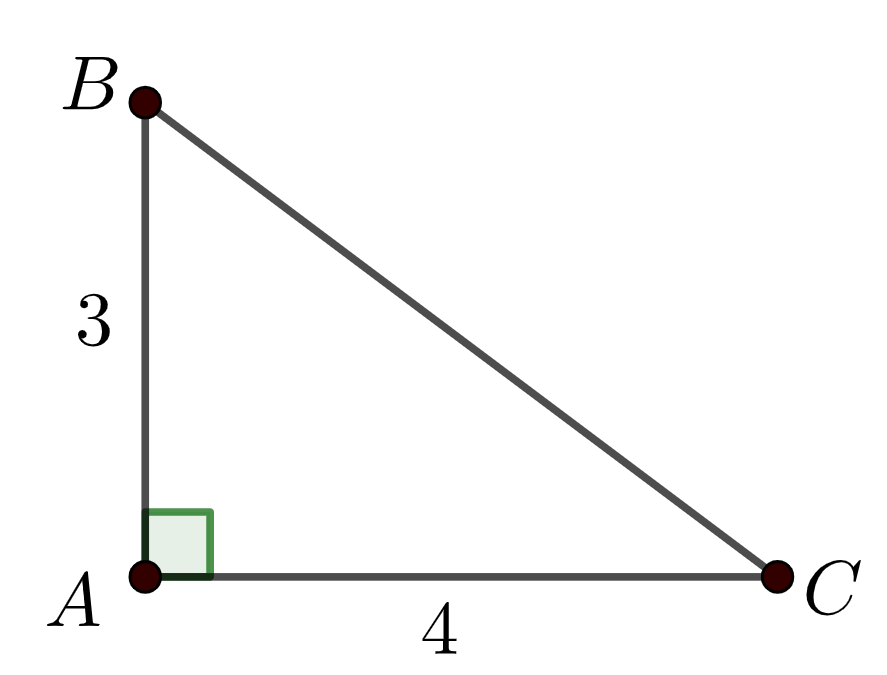
Основанием пирамиды является прямоугольный треугольник с катетами \(\displaystyle 3\) и \(\displaystyle 4{\small .}\) Высота пирамиды равна \(\displaystyle 5{\small.}\) Найдите объем этой пирамиды.
Обозначим через \(\displaystyle S\) вершину и через \(\displaystyle ABC\) – основание данной пирамиды.
Воспользуемся формулой для вычисления объема пирамиды.
Объём пирамиды
Объём пирамиды \(\displaystyle V\) равен одной трети произведения площади основания на высоту.
\(\displaystyle V=\frac{1}{3}S_{осн} \cdot h { \small ,} \)
где \(\displaystyle S_{осн} \) – площадь основания,
\(\displaystyle h\) – высота пирамиды.
Подставим \(\displaystyle S_{\triangle ABC}\) и \(\displaystyle h\) в формулу для вычисления объема пирамиды:
\(\displaystyle V=\frac{1}{3}S_{осн}\cdot h=\frac{1}{3}\cdot 6\cdot 5=10{\small. }\)
Ответ: \(\displaystyle 10{\small .}\)