Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно \(\displaystyle 3{\small .}\) Найдите объем пирамиды.
Пусть \(\displaystyle ABC\) – основание, \(\displaystyle S\) – вершина пирамиды.
1. По условию:
- боковые ребра взаимно перпендикулярны, то есть \(\displaystyle SA\perp SB{\small ,}\) \(\displaystyle SB\perp SC{\small ,}\) \(\displaystyle SA\perp SC{\small ;}\)
- боковые ребра равны \(\displaystyle 3{ \small ,} \) то есть \(\displaystyle SA=SB=SC=3{\small .}\)
2. Для вычисления объема пирамиды по формуле \(\displaystyle V=\frac{1}{3}S_{осн} \cdot h \) требуется знать площадь основания и высоту.
При этом в данном случае:
Значит, если взять \(\displaystyle SAC \) за основание, то \(\displaystyle SB\) будет высотой пирамиды. | 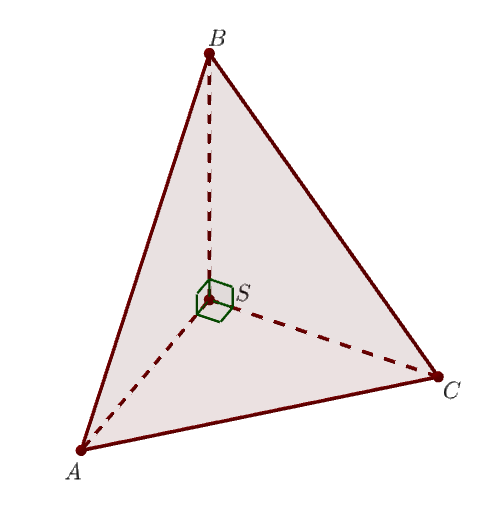 |
Таким образом, высота пирамиды равна
\(\displaystyle h=SB=3{\small .}\)
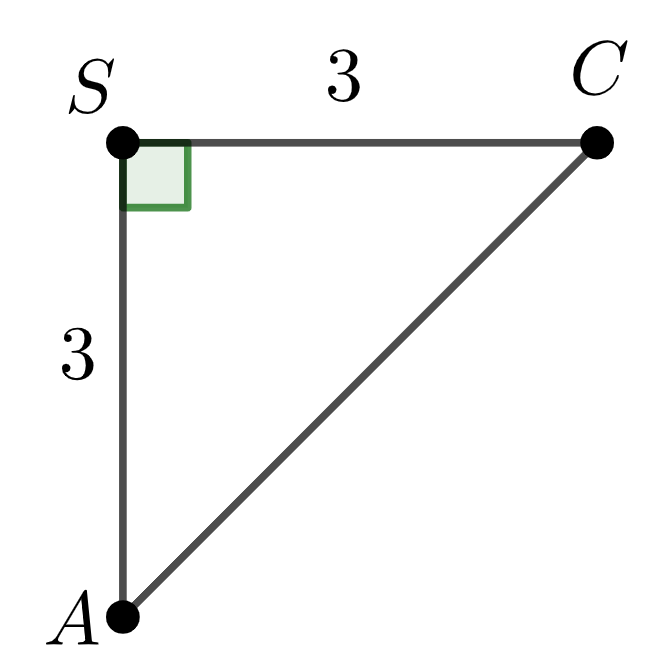
Площадь основания \(\displaystyle SAC \) равна
Подставим \(\displaystyle h\) и \(\displaystyle S_{осн}\) в формулу для объема пирамиды:
\(\displaystyle V=\frac{1}{3}S_{осн} \cdot h=\frac{1}{3}\cdot S_{\triangle SAC} \cdot SB = \frac{1}{3}\cdot \frac{9}{2}\cdot 3= 4{,}5{\small .}\)
Ответ: \(\displaystyle 4{,}5{\small .}\)
Чтобы строго доказать, что ребро \(\displaystyle SB\) перпендикулярно плоскости \(\displaystyle SAC{\small ,}\) воспользуемся признаком перпендикулярности прямой и плоскости.
Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
По условию \(\displaystyle SB\perp SA\) и \(\displaystyle SB\perp SC{\small .}\)
Прямые \(\displaystyle SA\) и \(\displaystyle SC\) пересекаются в точке \(\displaystyle S\) и лежат в плоскости \(\displaystyle SAC{\small .}\)
Следовательно, \(\displaystyle SB\) перпендикулярно плоскости \(\displaystyle SAC{\small .}\)