При пересечении прямых \(\displaystyle AB\), \(\displaystyle CD\) и \(\displaystyle EF\) в точке \(\displaystyle O\) образовались три пары вертикальных углов. Известно, что \(\displaystyle ∠ AOC\) в \(\displaystyle 3\) раза больше \(\displaystyle ∠ COE\), а \(\displaystyle ∠ AOF\) на \(\displaystyle 80^{\circ}\) больше \(\displaystyle ∠ COE\). Определите величины \(\displaystyle ∠ COE\), \(\displaystyle ∠ AOC\) и \(\displaystyle ∠ AOF\).
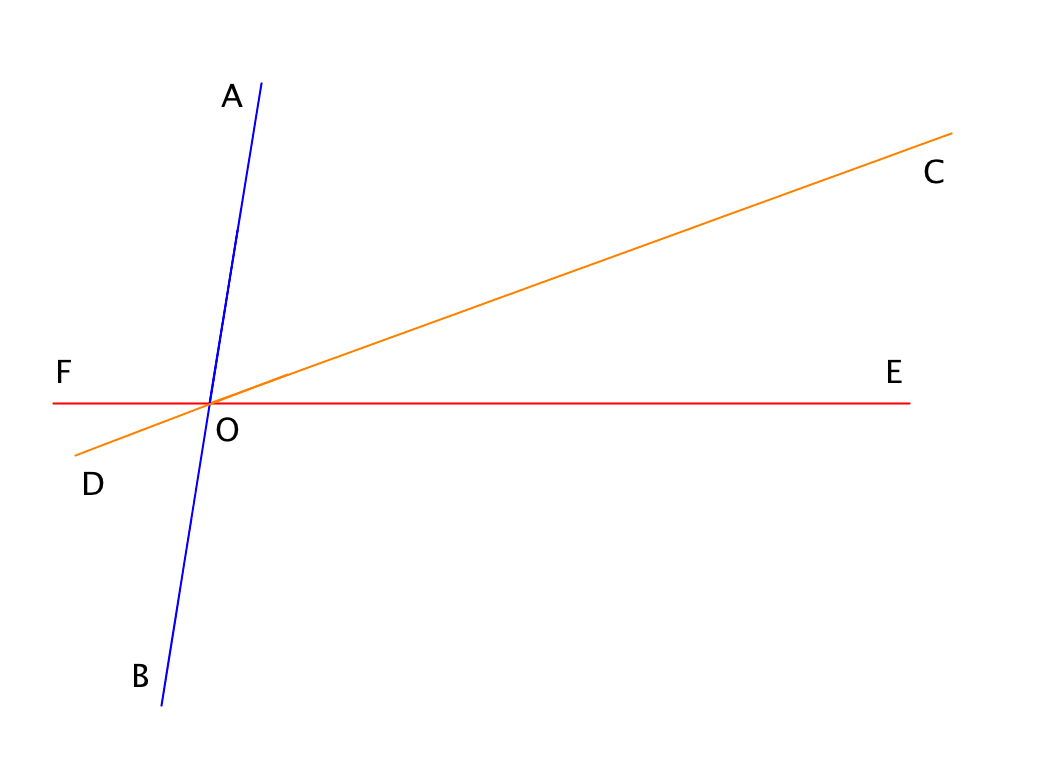
\(\displaystyle ∠ COE=\)\(\displaystyle ^{\circ}\);
\(\displaystyle ∠ AOC=\)\(\displaystyle ^{\circ}\);
\(\displaystyle ∠ AOF=\)\(\displaystyle ^{\circ}\)
Смежные и вертикальные углы. Свойства смежных и вертикальных углов
Внутри развернутого угла \(\displaystyle ABC\) проведен луч \(\displaystyle BD\). Он разбивает развернутый угол на два угла – \(\displaystyle ABD\) и \(\displaystyle DBC\), которые называются смежными углами.
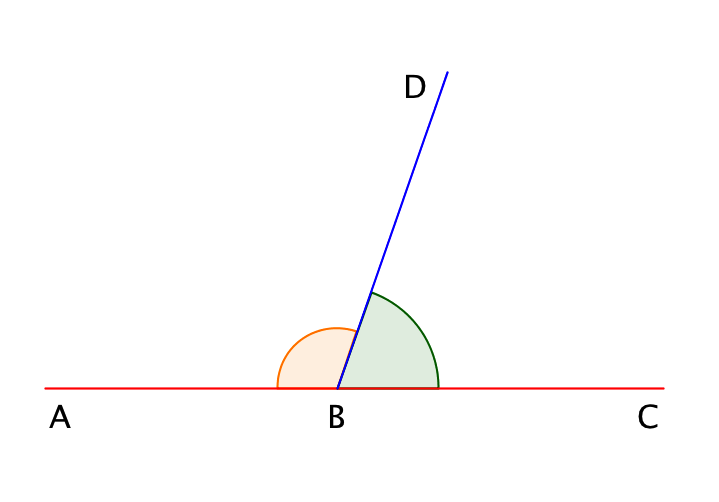
Сумма смежных углов равна \(\displaystyle 180\) градусов:
\(\displaystyle ∠ ABD+∠ DBC=180^{\circ}.\)
Если две прямые \(\displaystyle AB\) и \(\displaystyle CD\) пересекаются в точке \(\displaystyle O\), то углы \(\displaystyle AOC\) и \(\displaystyle BOD\) называются вертикальными. Другой парой вертикальных углов являются углы \(\displaystyle AOD\) и \(\displaystyle BOC\):
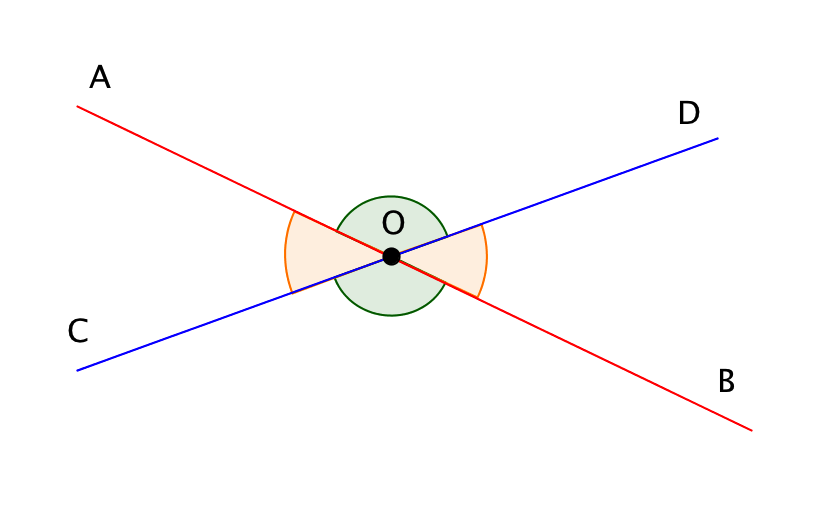
Вертикальные углы равны:
\(\displaystyle ∠ AOC=∠ BOD,\)
\(\displaystyle ∠ AOD=∠ BOC.\)
При пересечении прямых \(\displaystyle AB\), \(\displaystyle CD\) и \(\displaystyle EF\) в точке \(\displaystyle O\) образуются три пары вертикальных углов:
- \(\displaystyle ∠ AOF\) и \(\displaystyle ∠ BOE\);
- \(\displaystyle ∠ DOF\) и \(\displaystyle ∠ COE\);
- \(\displaystyle ∠ BOD\) и \(\displaystyle ∠ AOC\).
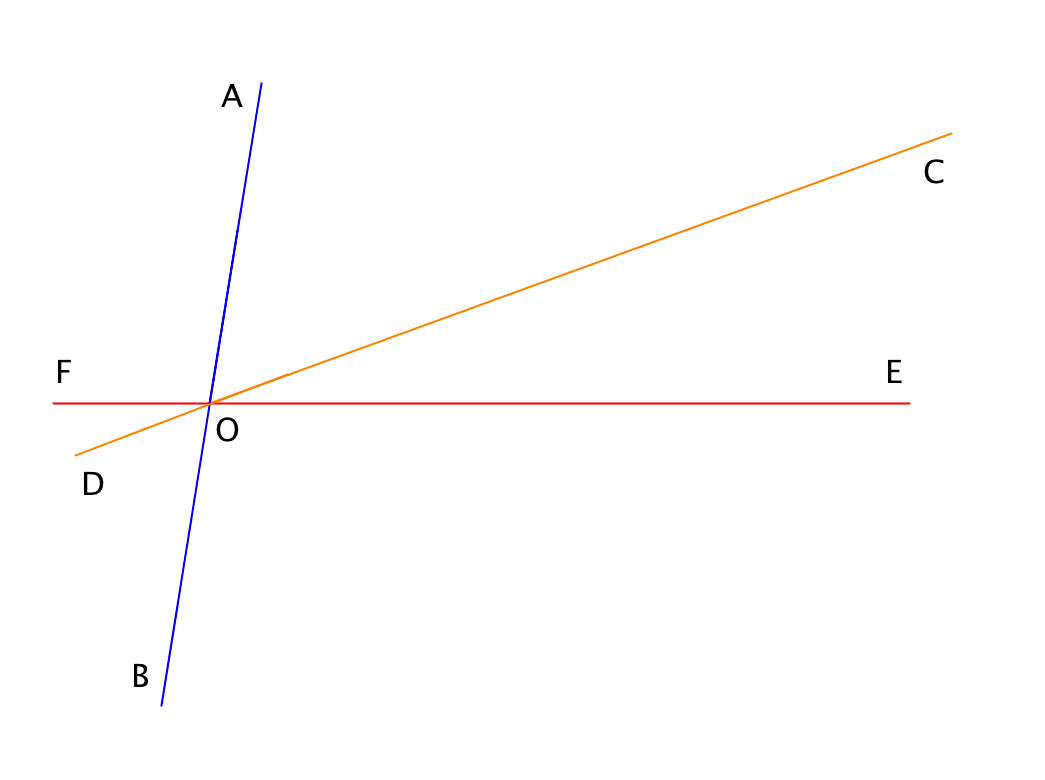
При этом
\(\displaystyle ∠ AOF=∠ BOE,\)
\(\displaystyle ∠ DOF=∠ COE,\)
\(\displaystyle ∠ BOD=∠ AOC.\)
Возьмем из каждой пары вертикальных углов по одному углу так, чтобы их сумма составляла развернутый угол. Например,
\(\displaystyle ∠ EOF=∠ COE+∠ AOC+∠ AOF=180^{\circ}.\)
Согласно условию, \(\displaystyle ∠ AOC\) в \(\displaystyle 3\) раза больше \(\displaystyle ∠ COE\), то есть
\(\displaystyle ∠ AOC=3 \cdot ∠ COE.\)
Также согласно условию, \(\displaystyle ∠ AOF\) на \(\displaystyle 80^{\circ}\) больше \(\displaystyle ∠ COE\), то есть
\(\displaystyle ∠ AOF=∠ COE+80^{\circ}.\)
Тогда
\(\displaystyle 180^{\circ}=∠ COE+3 \cdot ∠ COE+(∠ COE+80^{\circ}),\)
\(\displaystyle 5 \cdot ∠ COE=180^{\circ}-80^{\circ}=100^{\circ},\)
\(\displaystyle ∠ COE=\frac{100^{\circ}}{5}=20^{\circ}.\)
Значит,
\(\displaystyle ∠ AOC=3 \cdot ∠ COE=3 \cdot 20^{\circ}=60^{\circ},\)
\(\displaystyle ∠ AOF=∠ COE+80^{\circ}=20^{\circ}+80^{\circ}=100^{\circ}.\)
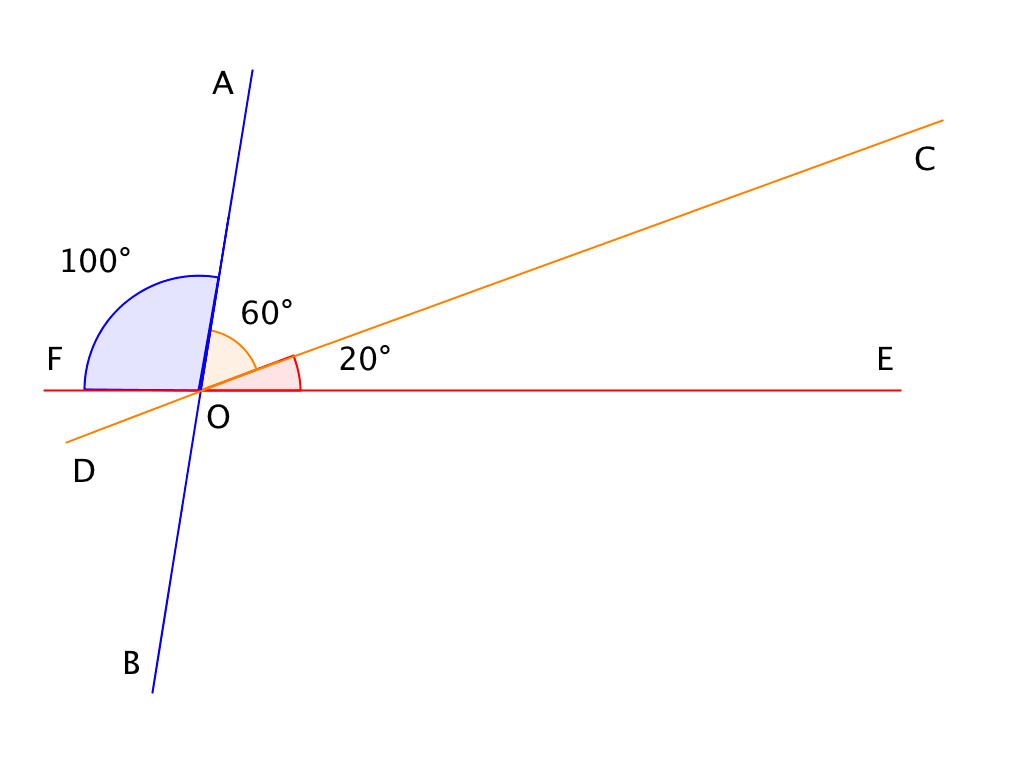
Выполним проверку:
\(\displaystyle ∠ EOF=∠ COE + ∠ AOC + ∠ AOF= 20^{\circ} + 60^{\circ} + 100^{\circ} = 180^{\circ}.\)
Ответ: \(\displaystyle ∠ COE=20^{\circ}\); \(\displaystyle ∠ AOC=60^{\circ}\); \(\displaystyle ∠ AOF=100^{\circ}\).