Прямые \(\displaystyle AD\) и \(\displaystyle BC\) пересекаются в точке \(\displaystyle O\). Найдите значения углов \(\displaystyle BOD\), \(\displaystyle COD\) и \(\displaystyle AOC\), если известно, что \(\displaystyle ∠ AOB=150^{\circ}.\)
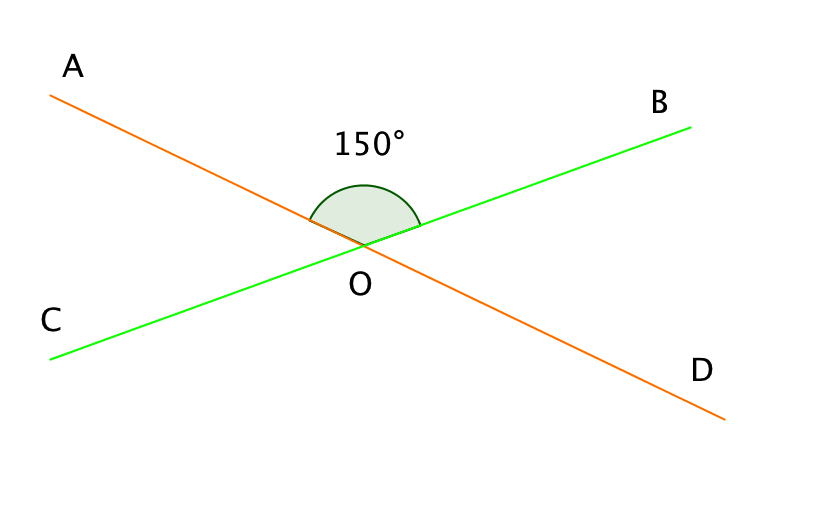
\(\displaystyle ∠ BOD=\) \(\displaystyle ^{\circ}\)
\(\displaystyle ∠ COD=\) \(\displaystyle ^{\circ}\)
\(\displaystyle ∠ AOC=\) \(\displaystyle ^{\circ}\)
Смежные и вертикальные углы. Свойства смежных и вертикальных углов
Внутри развернутого угла \(\displaystyle ABC\) проведен луч \(\displaystyle BD\). Он разбивает развернутый угол на два угла – \(\displaystyle ∠ ABD\) и \(\displaystyle ∠ DBC\), которые называются смежными углами.
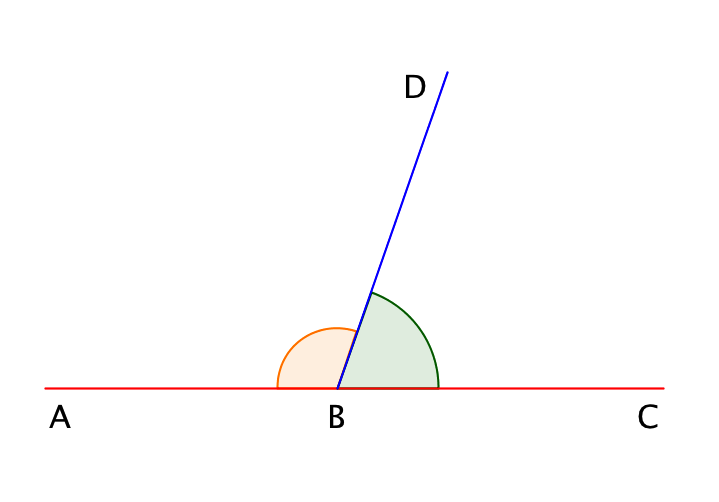
Сумма смежных углов равна \(\displaystyle 180\) градусов:
\(\displaystyle ∠ ABD+∠ DBC=180^{\circ}.\)
Если две прямые \(\displaystyle AB\) и \(\displaystyle CD\) пересекаются в точке \(\displaystyle O\), то углы \(\displaystyle AOC\) и \(\displaystyle BOD\) называются вертикальными. Другой парой вертикальных углов являются углы \(\displaystyle AOD\) и \(\displaystyle BOC\):
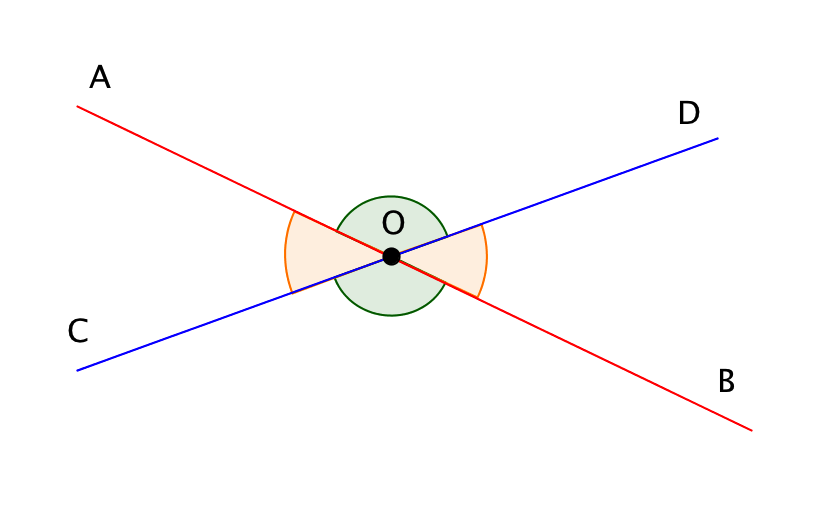
Вертикальные углы равны:
\(\displaystyle ∠ AOC=∠ BOD,\)
\(\displaystyle ∠ AOD=∠ BOC.\)
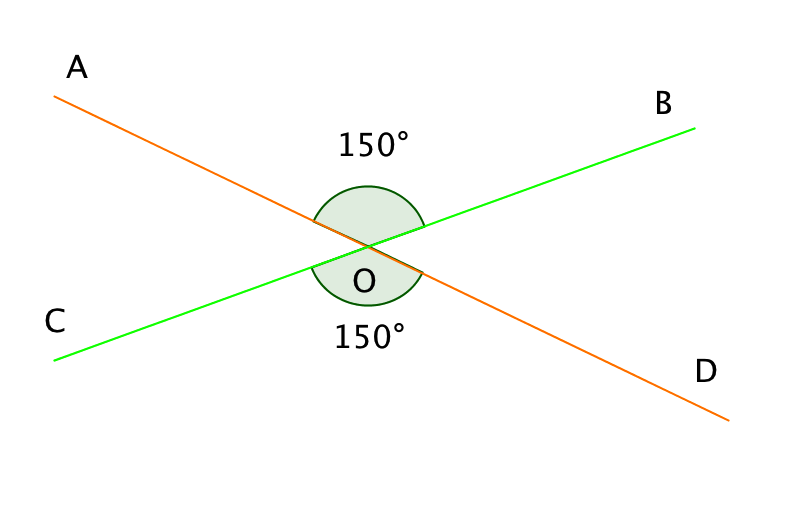
Так как углы \(\displaystyle AOB\) и \(\displaystyle BOD\) – смежные, то \(\displaystyle ∠ AOB+∠ BOD=180^{\circ}.\)
Следовательно,
\(\displaystyle ∠ BOD=180^{\circ} -∠ AOB=180^{\circ} - 150^{\circ}=30^{\circ}.\)
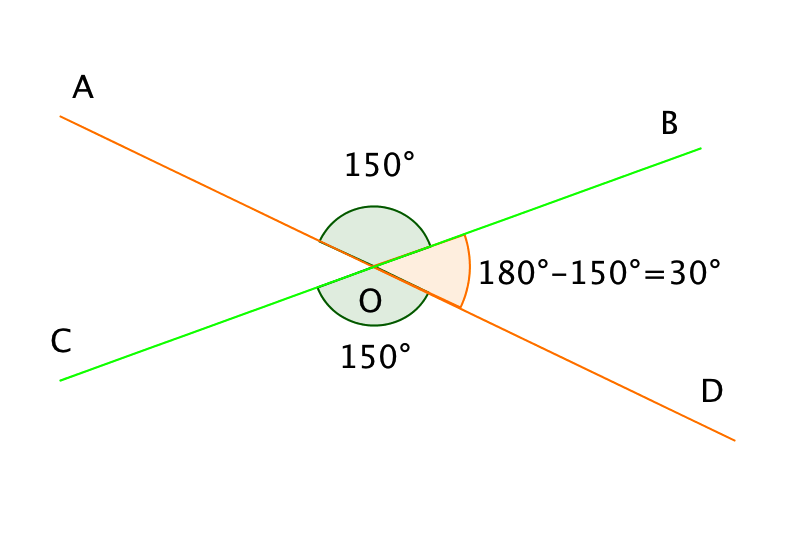
Так как углы \(\displaystyle BOD\) и \(\displaystyle AOC\) являются вертикальными, то \(\displaystyle ∠ AOC=∠ BOD=30^{\circ}.\)
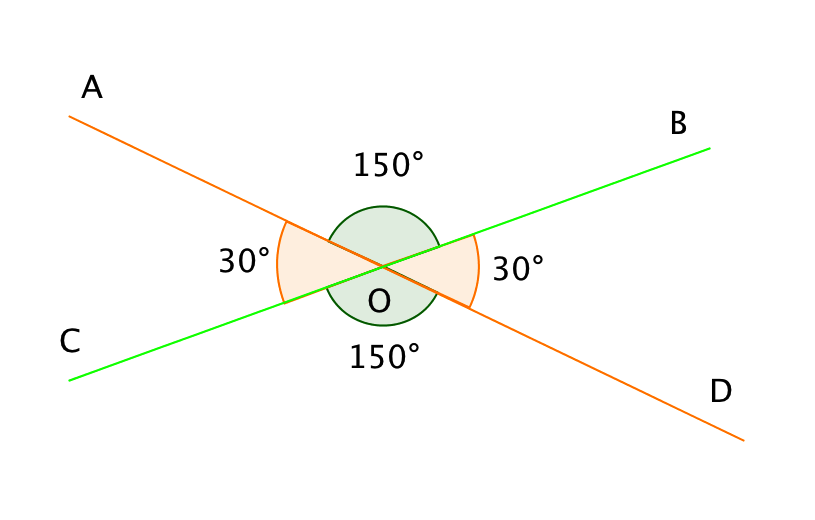
Ответ: \(\displaystyle ∠ BOD=30^{\circ}, ∠ COD=150^{\circ}, ∠ AOC=30^{\circ}.\)