Один из углов, образованных пересечением двух прямых, на \(\displaystyle 60^{\circ}\) больше другого. Сколько градусов составляет бóльший угол?
\(\displaystyle ^{\circ}\)
Смежные и вертикальные углы. Свойства смежных и вертикальных углов
Внутри развернутого угла \(\displaystyle ABC\) проведен луч \(\displaystyle BD\). Он разбивает развернутый угол на два угла – \(\displaystyle ABD\) и \(\displaystyle DBC\), которые называются смежными углами.
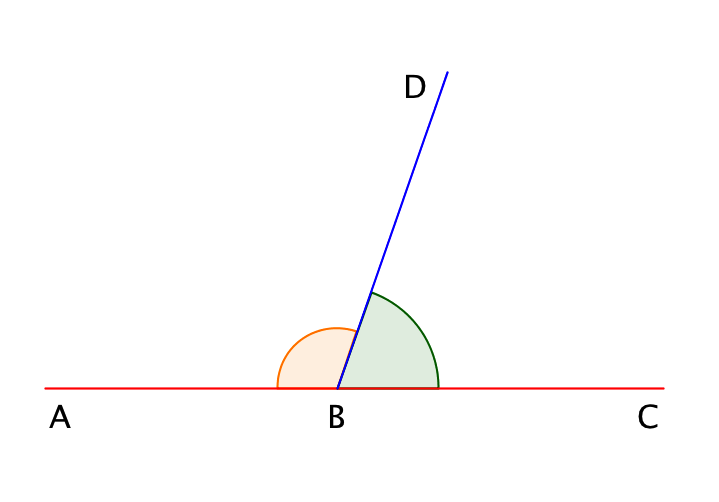
Сумма смежных углов равна \(\displaystyle 180\) градусов:
\(\displaystyle ∠ ABD+∠ DBC=180^{\circ}.\)
Если две прямые \(\displaystyle AB\) и \(\displaystyle CD\) пересекаются в точке \(\displaystyle O\), то углы \(\displaystyle AOC\) и \(\displaystyle BOD\) называются вертикальными. Другой парой вертикальных углов являются углы \(\displaystyle AOD\) и \(\displaystyle BOC\):
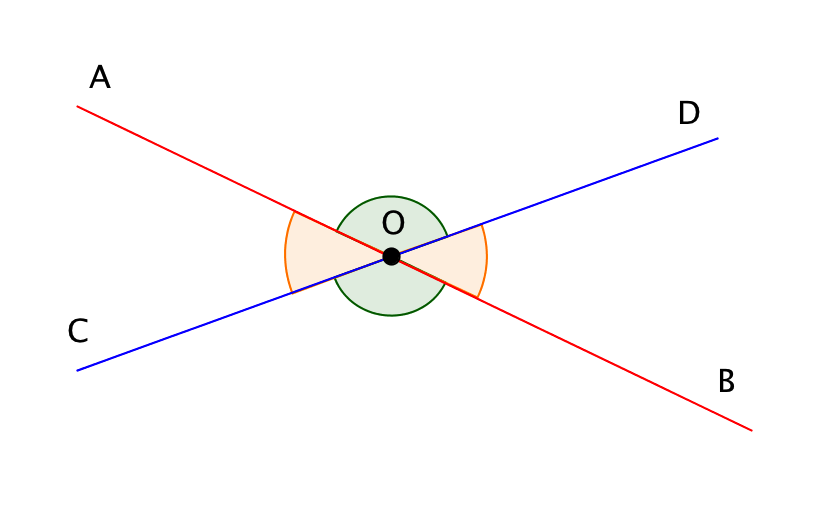
Вертикальные углы равны:
\(\displaystyle ∠ AOC=∠ BOD,\)
\(\displaystyle ∠ AOD=∠ BOC.\)
Пусть прямые \(\displaystyle AB\) и \(\displaystyle CD\) пересекаются в точке \(\displaystyle O\). При этом образуются четыре угла – это \(\displaystyle ∠ AOD\), \(\displaystyle ∠ BOD\), \(\displaystyle ∠ BOC\), \(\displaystyle ∠ AOC\):
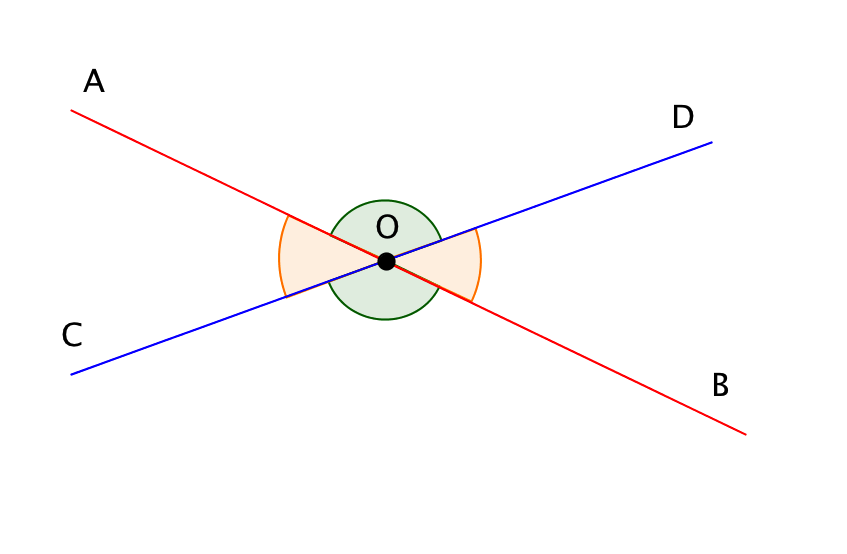
Согласно условию задачи, один из углов на \(\displaystyle 60^{\circ}\) больше другого. Поскольку вертикальные углы равны, то углы, о которых идет речь в условии, могут быть только смежными. Поэтому для решения задачи выберем любые два смежных угла – например, \(\displaystyle ∠ AOD\) и \(\displaystyle ∠ BOD\), и найдем, чему равен \(\displaystyle ∠ AOD\).
По условию, \(\displaystyle ∠ AOD\) на \(\displaystyle 60^{\circ}\) больше \(\displaystyle ∠ BOD\), то есть
\(\displaystyle ∠ AOD=∠ BOD+60^{\circ}.\)
Поскольку \(\displaystyle ∠ AOD\) и \(\displaystyle ∠ BOD\) – смежные, то
\(\displaystyle ∠ AOD+∠ BOD=180^{\circ}.\)
Тогда
\(\displaystyle ∠ BOD+∠ BOD+60^{\circ}=180^{\circ},\)
\(\displaystyle 2\cdot ∠ BOD=180^{\circ}-60^{\circ}=120^{\circ},\)
\(\displaystyle ∠ BOD=\frac{120^{\circ}}{2}=60^{\circ},\)
\(\displaystyle ∠ AOD=60^{\circ}+60^{\circ}=120^{\circ}.\)
Ответ: \(\displaystyle 120^{\circ}.\)