Төмендегі сызықтық теңдеу берілген:
\(\displaystyle -4x+12=0.\)
Суретте көрсетілген түзулердің қайсысы \(\displaystyle OX\) осімен қиылысқанда берілген сызықтық теңдеуді береді?
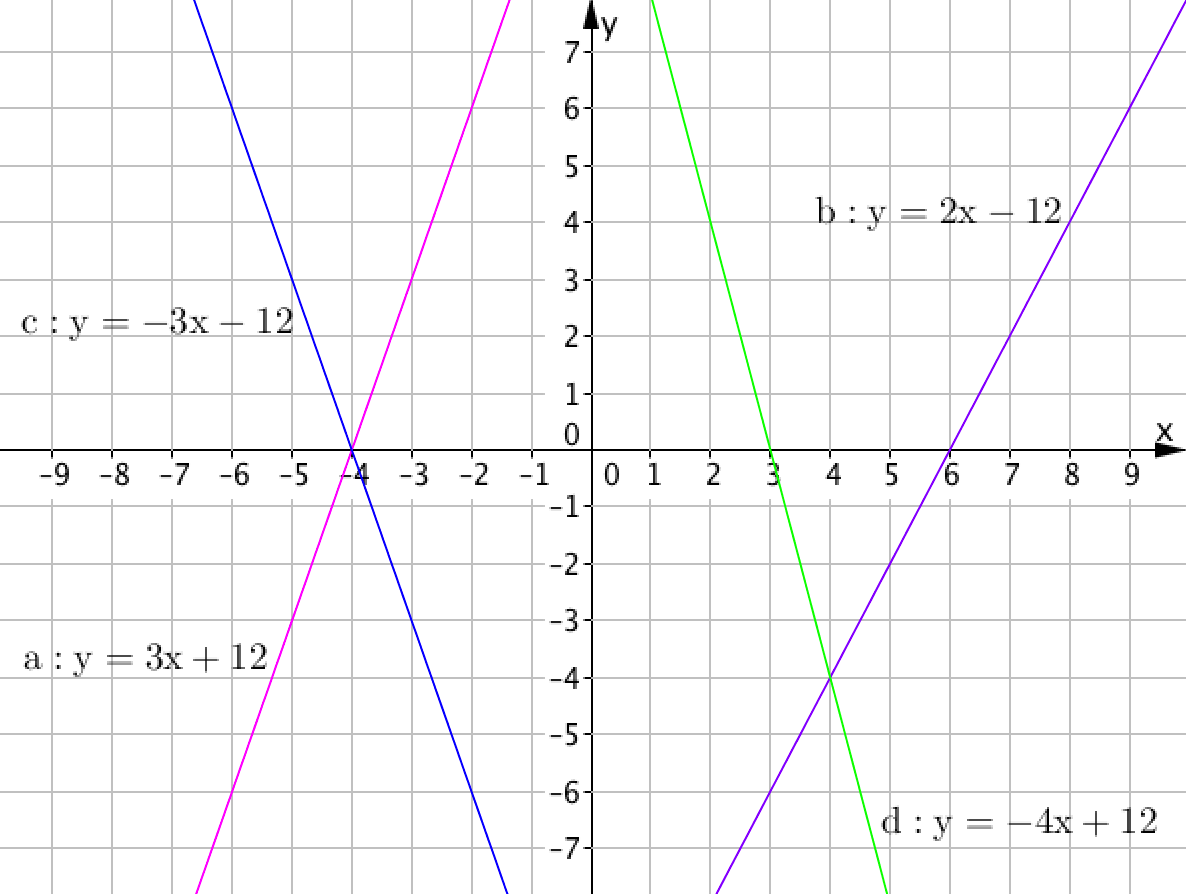
Бізге \(\displaystyle OX\) осі қиылысқан кезде \(\displaystyle -4x+12=0\) сызықтық теңдеуін беретін түзуді таңдау керек.
\(\displaystyle OX\) осімен қиылысқан кезде әрбір түзу беретін сызықтық теңдеулерді табайық. Ол үшін әр түзу теңдеудегі \(\displaystyle y\)-ті \(\displaystyle 0\)-ге ауыстырамыз:
- \(\displaystyle a:\, \color{blue}{y}=3x+12 \) түзуі \(\displaystyle \color{blue}{0}=3x+12\) сызықтық теңдеуін береді,
- \(\displaystyle b:\, \color{blue}{y}=2x-12 \) түзуі \(\displaystyle \color{blue}{0}=2x-12\) сызықтық теңдеуін береді,
- \(\displaystyle c:\, \color{blue}{y}=-3x-12 \) түзуі \(\displaystyle \color{blue}{0}=-3x-12\) сызықтық теңдеуін береді,
- \(\displaystyle d:\, \color{blue}{y}=-4x+12 \) түзуі \(\displaystyle \color{blue}{0}=-4x+12\) сызықтық теңдеуін береді,
Алынған сәйкестіктерден \(\displaystyle d:\, y={\bf -4x+12} \) түзуі берілген \(\displaystyle {\bf -4x+12}=0\) сызықтық теңдеуін береді.
Жауабы: \(\displaystyle d\) түзуі.
Берілген сызықтық теңдеуден түзу алу алгоритмі
\(\displaystyle OX\) осімен қиылысқан кезде \(\displaystyle y={\bf ax+b}\) түзуі \(\displaystyle {\bf ax+b}=0\)сызықтық теңдеуін береді.
Демек, \(\displaystyle {\bf ax+b}=0\) сызықтық теңдеуі бойынша берілген сызықтық теңдеуді беретін \(\displaystyle y={\bf ax+b} \) түзуін құруға болады деп айтуға болады.
Біздің жағдайда \(\displaystyle -4x+12=0\) сызықтық теңдеуі бойынша \(\displaystyle d: y=-4x+12\) түзуін құрамыз.