Skip to main content

Теориясы: \(\displaystyle \cos(2x)+\sin^2(x)=0{,}75\) теңдеуі

Тапсырма

Информация

Теңдеуі \(\displaystyle \cos(2x)+\sin^2(x)=0{,}75\) екі теңдеуге мәндес: 

\(\displaystyle \sin(x)=\frac{1}{2}\) немесе \(\displaystyle \sin(x)=-\frac{1}{2}{\small .}\)

\(\displaystyle \sin(x)=-\frac{1}{2}\) теңдеуінің шешімдері:

\(\displaystyle x_1=\frac{7\pi}{6}+2\pi n, \, n\in \mathbb{Z}\) және \(\displaystyle x_2=\frac{11\pi}{6}+2\pi n, \, n\in \mathbb{Z}{ \small .}\)

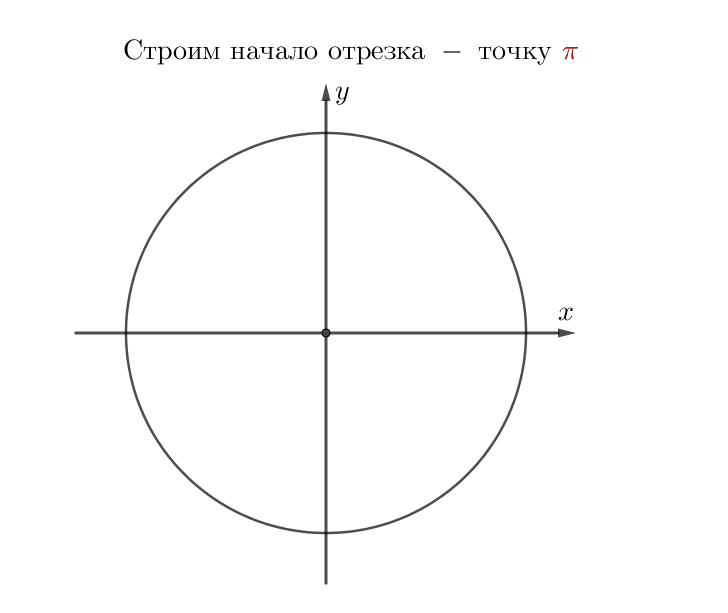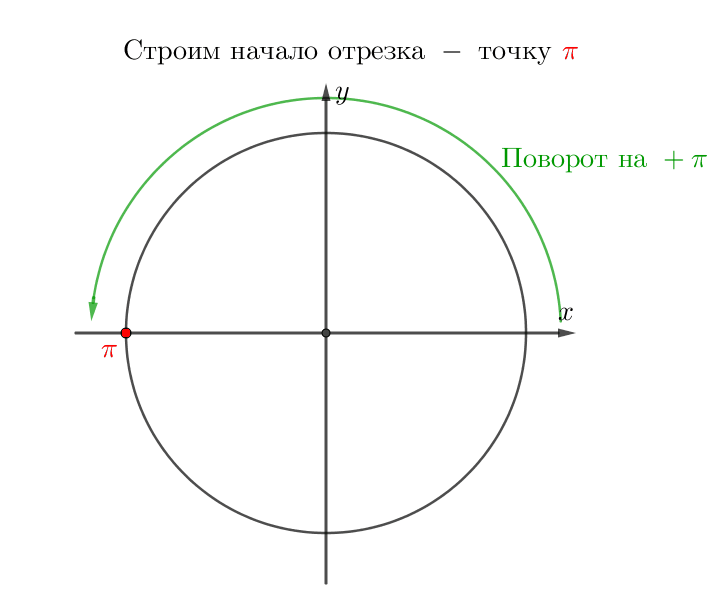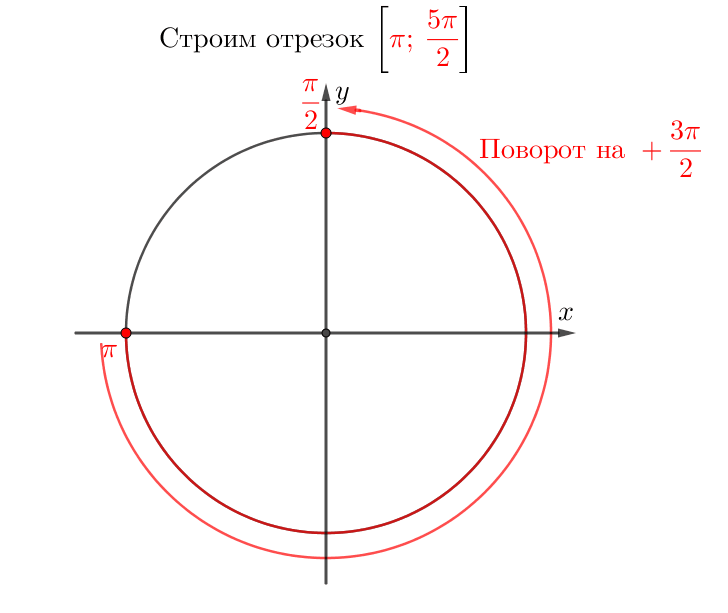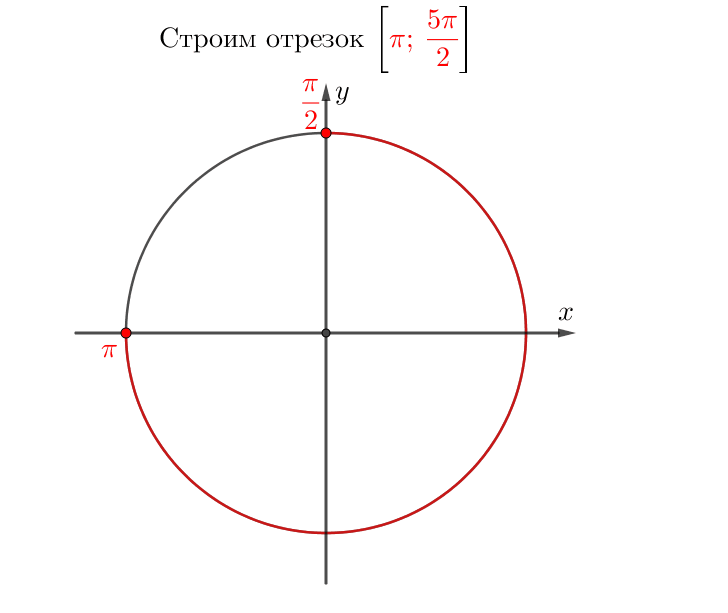
Теңдеудің түбірлерін  \(\displaystyle \sin(x)=-\frac{1}{2}\) аралықтан \(\displaystyle \left[\pi;\, \frac{5\pi}{2}\right]{\small}\) таңдаңыз

\(\displaystyle x_1=\frac{7\pi}{6}{\small,}\)

\(\displaystyle x_2=\frac{11\pi}{6}{\small.}\)

Шешім

\(\displaystyle \left[\pi;\, \frac{5\pi}{2}\right]{\small}\) кесіндіден түбірлерді таңдаймыз.

Тригонометриялық шеңбердегі кесіндіні таңдау.

\(\displaystyle x_1=\frac{7\pi}{6}+2\pi n\) үшін \(\displaystyle \frac{7\pi}{6}\) қолайлы шешім.

Пішіннің бір нүктесі \(\displaystyle \frac{7\pi}{6}+2\pi n\) поқажетті кесіндіге түсті:

Оны табайық.

 Біз \(\displaystyle n\) бүтін мәндерді іздейміз

\(\displaystyle \pi\leqslant x_1 \leqslant \frac{5\pi}{2}{ \small .}\)

 Яғни

\(\displaystyle \pi\leqslant \frac{7\pi}{6}+2\pi n \leqslant \frac{5\pi}{2}{ \small .}\)

 Теңсіздікті \(\displaystyle \pi{\small}\) оң санға бөлейік:

\(\displaystyle 1\leqslant \frac{7}{6}+2n\leqslant \frac{5}{2}{\small .}\)

 Әр бөліктен \(\displaystyle \frac{7}{6}{\small }\) алып тастаймыз:

\(\displaystyle 1- \frac{7}{6}\leqslant 2n\leqslant \frac{5}{2}- \frac{7}{6}{ \small ,}\)

\(\displaystyle -\frac{1}{6}\leqslant2n \leqslant \frac{4}{3}{ \small .}\)

 \(\displaystyle n{ \small}\) белгілеу үшін теңсіздіктерді \(\displaystyle 2{\small }\) бөлеміз:

\(\displaystyle -\frac{1}{12}\leqslant n \leqslant \frac{2}{3}{ \small .}\)

 Бұл аралықтағы жалғыз бүтін сан \(\displaystyle 0{\small,}\) яғни, \(\displaystyle n=0{\small .}\)

 \(\displaystyle n=0\) ауыстыру арқылы  \(\displaystyle \frac{7\pi}{6}+2\pi n{ \small,}\) аламыз:

\(\displaystyle \frac{7\pi}{6}+2\pi \cdot 0=\frac{7\pi}{6}{\small .}\)

\(\displaystyle x_2=\frac{11\pi}{6}+2\pi n\) үшін \(\displaystyle \frac{11\pi}{6}\) қолайлы шешім.

Пішіннің бір нүктесі \(\displaystyle \frac{11\pi}{6}+2\pi n\) қажетті кесіндіге түсті:

Оны табайық.

 Біз \(\displaystyle n\) бүтін мәндерді іздейміз

\(\displaystyle \pi\leqslant x_2 \leqslant \frac{5\pi}{2}{ \small .}\)

 Яғни

\(\displaystyle \pi\leqslant \frac{11\pi}{6}+2\pi n \leqslant \frac{5\pi}{2}{ \small .}\)

 Теңсіздікті \(\displaystyle \pi{\small}\) оң санға бөлейік:

\(\displaystyle 1\leqslant \frac{11}{6}+2n\leqslant \frac{5}{2}{\small .}\)

 Әр бөліктен \(\displaystyle \frac{11}{6}{\small}\) алып тастаймыз:

\(\displaystyle 1- \frac{11}{6}\leqslant 2n\leqslant \frac{5}{2}- \frac{11}{6}{ \small ,}\)

\(\displaystyle -\frac{5}{6}\leqslant2n \leqslant \frac{2}{3}{ \small .}\)

 \(\displaystyle n{ \small}\) белгілеу үшін теңсіздіктерді \(\displaystyle 2{\small}\) бөлеміз:

\(\displaystyle -\frac{5}{12}\leqslant n \leqslant \frac{1}{3}{ \small .}\)

 Бұл аралықтағы жалғыз бүтін сан \(\displaystyle 0{\small,}\) яғни, \(\displaystyle n=0{\small .}\)

 \(\displaystyle n=0\) ауыстыру арқылы  \(\displaystyle \frac{11\pi}{6}+2\pi n{ \small ,}\) аламыз:

\(\displaystyle \frac{11\pi}{6}+2\pi \cdot 0=\frac{11\pi}{6}{\small .}\)

Осылайша, \(\displaystyle \sin(x)=-\frac{1 }{2}\) теңдеуі \(\displaystyle \left[\pi;\, \frac{5\pi}{2}\right]\) кесіндісінде  \(\displaystyle \frac{7\pi}{6}\) және \(\displaystyle \frac{11\pi}{6}{\small}\) шешімдері бар.

Жауабы: \(\displaystyle \frac{7\pi}{6}\) және \(\displaystyle \frac{11\pi}{6}{\small .}\)