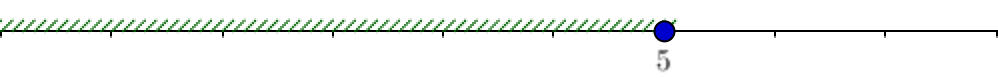Решите неравенство:
\(\displaystyle x^4-61x^2+900 \ge 0{\small .}\)
Представим \(\displaystyle x^4\) как \(\displaystyle (x^2)^2\) в биквадратном трехчлене \(\displaystyle x^4-61x^2+900{\small : } \)
\(\displaystyle x^4-61x^2+900= (\color{blue}{ x^2})^2-61\color{blue}{ x^2}+900{\small .} \)
Сделаем замену \(\displaystyle t=\color{blue}{ x^2}{ \small .} \) Получаем многочлен второй степени:
\(\displaystyle t^2-61t+900{\small .} \)
Найдем его корни и разложим на множители.
Получили неравенство \(\displaystyle (t-36)(t-25)\ge 0{\small .} \) Решим это неравенство.
Поскольку \(\displaystyle t=x^2{ \small ,} \) то, возвращаясь к переменной \(\displaystyle x{ \small ,} \) получаем объединение неравенств
\(\displaystyle x^2\le 25 \) или \(\displaystyle x^2\ge 36{\small .} \)
Решим эти неравенства.
Объединим решения неравенств \(\displaystyle x^2\le 25\) и \(\displaystyle x^2\ge 36{\small .}\)
Тогда \(\displaystyle x\in [-5;5] \) или \(\displaystyle x\in (-\infty;-6]\cup [6;+\infty){\small :} \)

Объединяя, получаем ответ:
\(\displaystyle x\in (-\infty;-6]\cup [-5;5]\cup [6;+\infty){\small .} \)
Ответ: \(\displaystyle x\in (-\infty;-6]\cup [-5;5]\cup [6;+\infty){\small .} \)