\(\displaystyle x^4\) \(\displaystyle x^4-61x^2+900\ \) биквадрат үшмүшесіндегі \(\displaystyle (x^2)^2\) түрінде көрсетейік
\(\displaystyle x^4-61x^2+900= (\color{blue}{ x^2})^2-61\color{blue}{ x^2}+900{\small .} \)
\(\displaystyle t=\color{blue}{ x^2}{ \small } \) ауыстыруды жасайық Екінші дәрежелі көпмүшені аламыз:
\(\displaystyle t^2-61t+900\ . \)
Оның түбірлерін тауып, көбейткіштерге жіктейік.
\(\displaystyle t^2-61t+900=(t-36)(t-25) \)
Коэффициенттерді бөліп алайық:
\(\displaystyle t^2-61t+900=\color{red}{ 1}\cdot t^2\color{green}{ -61}t+\color{blue}{ 900}{\small .}\)
Сонда \(\displaystyle \color{red}{ a}=\color{red}{ 1}, \color{green}{ b}=\color{green}{ -61}, \color{blue}{ c}=\color{blue}{ 900}{\small .} \)
Квадрат теңдеуді шешейік:
\(\displaystyle t^2-61t+900=0 \ . \)
Дискриминант:
\(\displaystyle {\rm D}= (\color{green}{-61})^2-4\cdot \color{red}{ 1}\cdot \color{blue}{ 900}=3721-3600=121\)
және
\(\displaystyle \sqrt{\rm D}=\sqrt{ 121}=11{\small .} \)
Теңдеудің түбірлері:
\(\displaystyle t_1= \frac{-(-61)+11}{2}=\frac{72}{2}=36{ \small ,}\)
\(\displaystyle t_2= \frac{-(-61)-11}{2}=\frac{50}{2}=25{\small .}\)
Ережеге сәйкес екінші дәрежелі көпмүшені көбейткіштерге жіктейік.
ЕрежеКөбейткіштерге жіктеу
\(\displaystyle \color{red}{ a}t^2+bt+c=\color{red}{ a}(t-t_1)(t-t_2){ \small ,}\)
мұндағы \(\displaystyle t_1 \) және \(\displaystyle t_2 \) –
\(\displaystyle \color{red}{ a}t^2+bt+c=0{\small .}\)
квадрат теңдеуінің түбірлері .
Біздің жағдайда үлкен коэффициент \(\displaystyle \color{red}{ a}=\color{red}{ 1}{ \small ,} \) ал түбірлері \(\displaystyle 36\) және \(\displaystyle 25\ \) тең
Демек,
\(\displaystyle t^2-61t+900=\color{red}{ 1}\cdot (t-36)(t-4)=(t-36)(t-25) {\small .}\)
\(\displaystyle (t-36)(t-25)\ge 0{\small } \) теңсіздігін алдық Бұл теңсіздікті шешейік.
\(\displaystyle (t-36)(t-25)\ge 0 \) теңсіздігі \(\displaystyle t\le 25 \) немесе \(\displaystyle t\ge 36\) шешімдеріне ие
\(\displaystyle (t-36)(t-25)\ge 0\) теңсіздігінің барлық шешімдері келесі жағдайларда алынады
- не \(\displaystyle t-36\ge 0 \ ,\, t-25\ge 0\) – екі көбейткіш те теріс емес;
- не \(\displaystyle t-36\le 0 \ ,\, t-25\le 0\) – екі көбейткіш те оң емес.
Егер оны жүйе түрінде қайта жазсақ, онда:
\(\displaystyle \left\{\begin{aligned}t-36&\ge 0{ \small ,}\\t-25&\ge 0\end{aligned}\right.\) немесе \(\displaystyle \left\{\begin{aligned}t-36&\le 0{ \small ,}\\t-25& \le 0{\small .}\end{aligned}\right.\)
Сызықтық теңсіздіктерді түрлендіру арқылы төмендегілерді аламыз:
\(\displaystyle \left\{\begin{aligned}t&\ge 36{ \small ,}\\t&\ge 25\end{aligned}\right.\) немесе \(\displaystyle \left\{\begin{aligned}t&\le 36{ \small ,}\\t& \le 25{\small .}\end{aligned}\right.\)
Алынған жүйелерді шешейік.
\(\displaystyle \left\{ \begin{aligned} t&\ge 36{ \small ,}\\ t&\ge 25 \end{aligned} \right.\) \(\displaystyle t\ge 36\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді: 
\(\displaystyle t\ge 25\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді:

Осылайша, \(\displaystyle t\) айнымалысы бір уақытта \(\displaystyle 36\) артық не тең және \(\displaystyle 25\ \) артық не тең 
Алынған қиылысу теңсіздіктердің бастапқы жүйесінің шешімі болады. Демек, шешім – \(\displaystyle t\in [36;+\infty){\small .} \) Немесе теңсіздік түрінде жазу арқылы, \(\displaystyle t\ge 36\ . \)
| немесе | \(\displaystyle \left\{ \begin{aligned} t&\le 36{ \small ,}\\ t& \le 25 \end{aligned} \right.\) \(\displaystyle t\le 36\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді: 
\(\displaystyle t\le 25\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді:

Осылайша, \(\displaystyle t\) айнымалысы бір уақытта \(\displaystyle 36\) кем не тең және \(\displaystyle 25\ \) кем не тең 
Алынған қиылысу теңсіздіктердің бастапқы жүйесінің шешімі болады. Демек, шешім – \(\displaystyle t\in (-\infty;25]{\small .} \) Немесе теңсіздік түрінде жазу арқылы, \(\displaystyle t\le 25{\small .} \) |
Алынған шешімдерді біріктіре отырып, төмендегілерді аламыз:
\(\displaystyle t\le 25\) немесе \(\displaystyle t\ge 36{\small .} \)
\(\displaystyle t=x^2 \ , \) болғандықтан \(\displaystyle x{ \small ,} \) айнымалысына орала отырып, келесі теңсіздіктердің бірігуін аламыз
\(\displaystyle x^2\le 25 \) немесе \(\displaystyle x^2\ge 36\ . \)
Бұл теңсіздіктерді шешейік.
\(\displaystyle x^2\le 25\) теңсіздігі\(\displaystyle x\in [-5;5] \) шешімдеріне ие
\(\displaystyle x^2\le 25\ \) теңсіздігін түрлендірейік
\(\displaystyle x^2\le 25 \ , \)
\(\displaystyle x^2-25\le 0 \ , \)
\(\displaystyle x^2-2^2\le 0 \ , \)
\(\displaystyle (x-5)(x+5)\le 0\ . \)
Алынған теңсіздікті эквивалентті теңсіздіктер жүйесі түрінде жазайық:
\(\displaystyle \left\{\begin{aligned}x-5&\ge 0{ \small ,}\\x+5&\le 0\end{aligned}\right.\) немесе \(\displaystyle \left\{\begin{aligned}x-5&\le 0{ \small ,}\\x+5& \ge 0{\small .}\end{aligned}\right.\)
Сызықтық теңсіздіктерді түрлендіру арқылы төмендегілерді аламыз:
\(\displaystyle \left\{\begin{aligned}x&\ge 5{ \small ,}\\x&\le -5\end{aligned}\right.\) немесе \(\displaystyle \left\{\begin{aligned}x&\le 5{ \small ,}\\x& \ge -5{\small .}\end{aligned}\right.\)
Алынған жүйелерді шешейік.
\(\displaystyle \left\{ \begin{aligned} x&\ge 5{ \small ,}\\ x&\le -5 \end{aligned} \right.\) \(\displaystyle x\ge 5\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді: 
\(\displaystyle x\le -5\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді:

Осылайша, \(\displaystyle x\) айнымалысы бір уақытта \(\displaystyle 5\) артық не тең және \(\displaystyle -5\ \) кем не тең 
Қиылысуда ортақ нүктелер болмағандықтан, теңсіздіктер жүйесінде шешімдер жоқ. Демек, шешімдер жиыны бос.
| немесе | \(\displaystyle \left\{ \begin{aligned} x&\le 5{ \small ,}\\ x& \ge -5 \end{aligned} \right.\) \(\displaystyle x\le 5\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді: 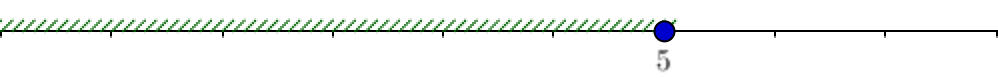
\(\displaystyle x\ge -5\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді:

Осылайша, \(\displaystyle x\) айнымалысы бір уақытта \(\displaystyle 5\) кем не тең және \(\displaystyle -5\ \) артық не тең 
Алынған қиылысу теңсіздіктердің бастапқы жүйесінің шешімі болады. Демек, шешім – \(\displaystyle x\in [-5;5]{\small .} \) |
Алынған шешімдерді біріктіре отырып, төмендегілерді аламыз:
\(\displaystyle x\in [-5;5]{\small .} \)
\(\displaystyle x^2\ge 36\) теңсіздігі \(\displaystyle x\in (-\infty;-6]\cup [ 6;+\infty) \) шешімдеріне ие
\(\displaystyle x^2\ge 36\ \) теңсіздігін түрлендірейік
\(\displaystyle x^2\ge 36 \ , \)
\(\displaystyle x^2-36\ge 0 \ , \)
\(\displaystyle x^2-6^2\ge 0 \ , \)
\(\displaystyle (x-6)(x+6)\ge 0\ . \)
Алынған теңсіздікті эквивалентті теңсіздіктер жүйесі түрінде жазайық:
\(\displaystyle \left\{\begin{aligned}x-6&\ge 0{ \small ,}\\x+6&\ge 0\end{aligned}\right.\) немесе \(\displaystyle \left\{\begin{aligned}x-6&\le 0{ \small ,}\\x+6& \le 0{\small .}\end{aligned}\right.\)
Сызықтық теңсіздіктерді түрлендіру арқылы төмендегілерді аламыз:
\(\displaystyle \left\{\begin{aligned}x&\ge 6{ \small ,}\\x&\ge -6\end{aligned}\right.\) немесе \(\displaystyle \left\{\begin{aligned}x&\le 6{ \small ,}\\x& \le -6{\small .}\end{aligned}\right.\)
Алынған жүйелерді шешейік.
\(\displaystyle \left\{ \begin{aligned} x&\ge 6{ \small ,}\\ x&\ge -6 \end{aligned} \right.\) \(\displaystyle x\ge 6\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді: 
\(\displaystyle x\ge -6\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді:

Осылайша, \(\displaystyle x\) айнымалысы бір уақытта \(\displaystyle 6\) артық не тең және \(\displaystyle -6\ \) артық не тең 
Алынған қиылысу теңсіздіктердің бастапқы жүйесінің шешімі болады. Демек, шешім – \(\displaystyle x\in [6;+\infty){\small .} \)
| немесе | \(\displaystyle \left\{ \begin{aligned} x&\le 6{ \small ,}\\ x& \le -6 \end{aligned} \right.\) \(\displaystyle x\le 6\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді: 
\(\displaystyle x\le -6\) теңсіздігі түзудегі нүктелер жиынына сәйкес келеді:

Осылайша, \(\displaystyle x\) айнымалысы бір уақытта \(\displaystyle 6\) кем не тең және \(\displaystyle -6\ \) кем не тең 
Алынған қиылысу теңсіздіктердің бастапқы жүйесінің шешімі болады. Демек, шешім –\(\displaystyle x\in (-\infty;-6]{\small .} \) |
Алынған шешімдерді біріктіре отырып, төмендегілерді аламыз:
\(\displaystyle x\in (-\infty;-6]\cup [6;+\infty){\small .} \)
\(\displaystyle x^2\le 25\) және \(\displaystyle x^2\ge 36\ \) теңсіздіктер шешімдерін біріктірейік
Сонда \(\displaystyle x\in [-5;5] \) немесе \(\displaystyle x\in (-\infty;-6]\cup [6;+\infty)\ : \)

Біріктіру арқылы келесі жауап аламыз:
\(\displaystyle x\in (-\infty;-6]\cup [-5;5]\cup [6;+\infty)\ . \)
Жауабы: \(\displaystyle x\in (-\infty;-6]\cup [-5;5]\cup [6;+\infty)\ . \)