Функцияның \(\displaystyle y=0{,}3(x-1)^2+2{\small }\) графигін таңдаңыз
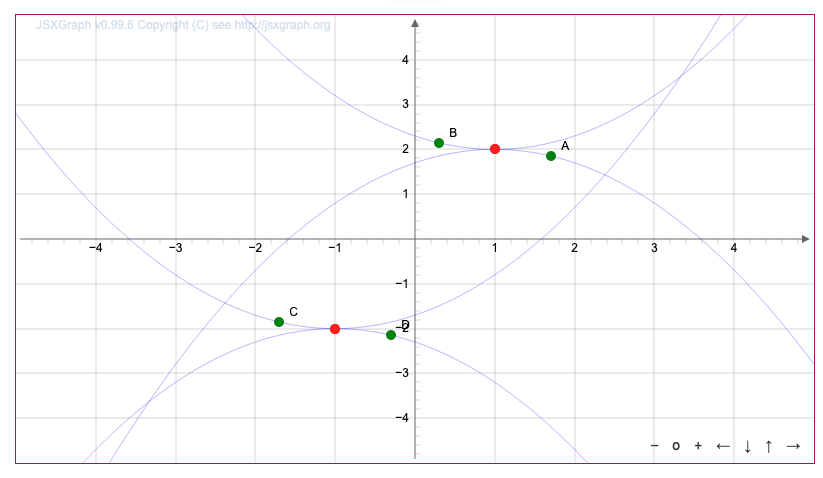
Осы параболалардың әрқайсысының белгілі шыңы бар:
параболаның \(\displaystyle \rm A\) нүктесінде \(\displaystyle (1;2){\small }\) шыңы бар,
параболаның \(\displaystyle \rm В\) нүктесінде \(\displaystyle (1;2){\small }\) шыңы бар,
параболаның \(\displaystyle \rm D\) нүктесінде \(\displaystyle (-1;-2){\small }\) шыңы бар,
параболаның \(\displaystyle \rm C\) нүктесінде \(\displaystyle (-1;-2){\small }\) шыңы бар.
Анықтамасы бойынша
\(\displaystyle y=k(x-a)^2+b\) теңдеуімен берілген параболаның шыңы
\(\displaystyle y=k(x-a)^2+b{ \small ,}\) теңдеуімен берілген параболаның шыңы \(\displaystyle (a;\,b){\small}\) координаталары бар нүкте.
\(\displaystyle y=0{,}3(x-1)^2+2{ \small ,}\) теңдеуімен берілген параболаның \(\displaystyle (1;2){\small }\) нүктесінде шыңы бар.
Бұл \(\displaystyle \rm A\) және \(\displaystyle \rm B{\small }\) графиктеріне сәйкес келеді.
\(\displaystyle k=0{,}3>0{\small ,}\) коэффициенті болғандықтан, қажетті параболаның тармақтары жоғары бағытталған болуы керек.
Парабола тармақтары \(\displaystyle \rm A\) төмен бағытталған.
Парабола тармақтары \(\displaystyle \rm В\) жоғары бағытталған.
Сонымен \(\displaystyle y=0{,}3(x-1)^2+2\) теңдеу \(\displaystyle \rm В{\small .}\) графигіне сәйкес келеді.
Жауабы:\(\displaystyle \rm В{\small .}\)