Параболаның шыңын \(\displaystyle O\) жылжыту арқылы \(\displaystyle y=3x^2{ \small }\) функциясын \(\displaystyle y=3(x-1)^2+1{\small }\) сызыңыз.
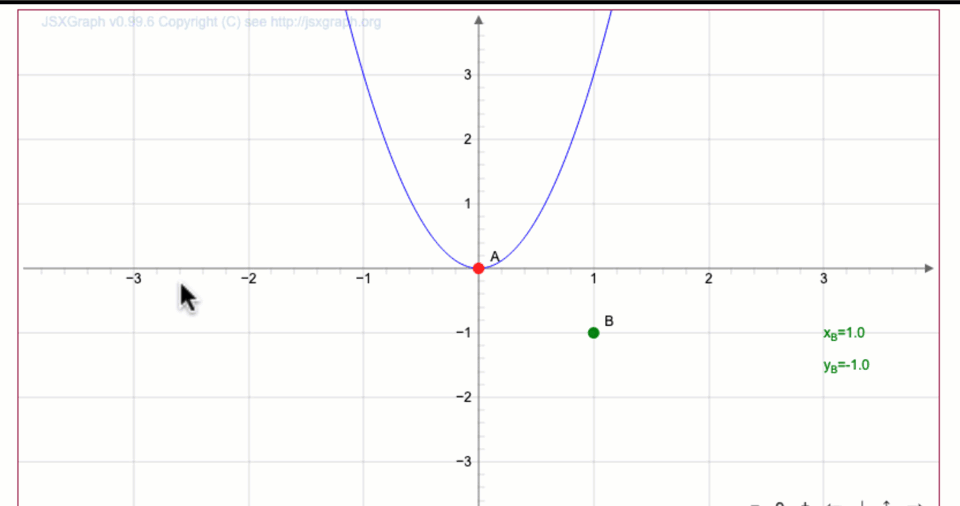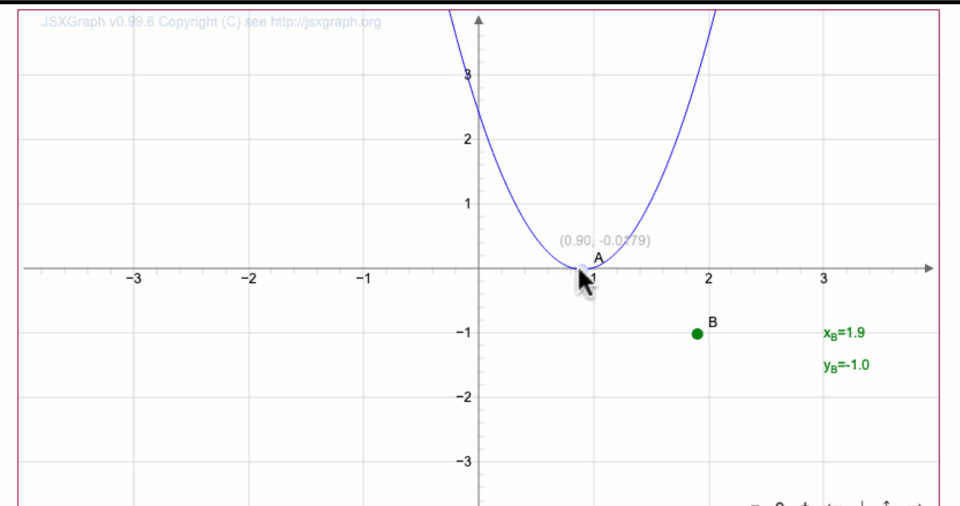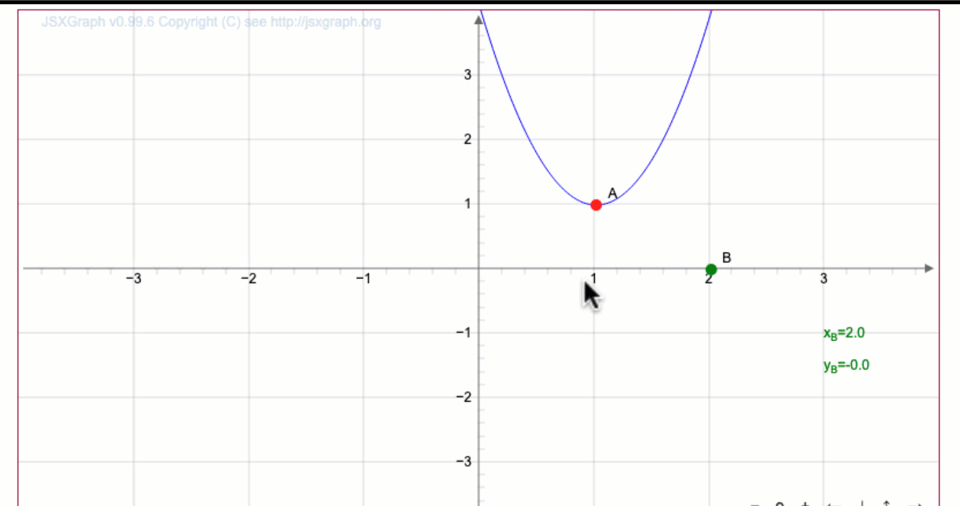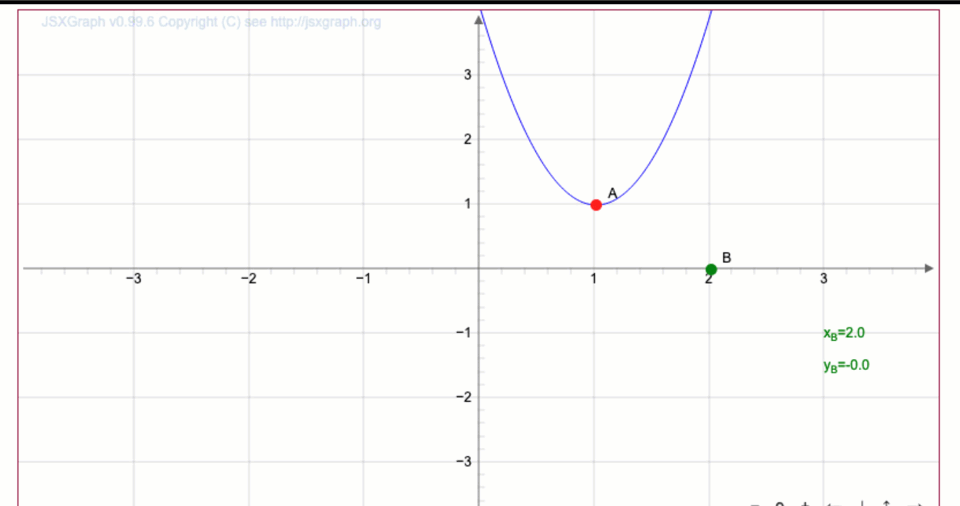
Алынған қисыққа \(\displaystyle \color{green}{В}\) нүктесінің координаталарын жазыңыз
\(\displaystyle \color{green}{В}=(\)\(\displaystyle \, ;\)\(\displaystyle )\)
ондыққа дейін дәл
Функция графигі \(\displaystyle y=k(x-a)^2+b\) парабола графигінен алынған \(\displaystyle y=kx^2\)
- әрбір \(\displaystyle a\) нүктені ось бойымен оңға \(\displaystyle \rm OX{\small }\) бірлікке жылжыту арқылы,
- әрбір \(\displaystyle b\) нүктені ось бойымен \(\displaystyle \rm OY{\small }\) бір жоғары жылжыту арқылы.
Сонда параболаның шыңы \(\displaystyle y=kx^2\) \(\displaystyle (0;\,0)\) нүктесі \(\displaystyle (0+a;0+b)=(a;\,b){\small }\) нүктесіне шығады.
\(\displaystyle y=k(x-a)^2+b\ \) теңдеуімен берілген параболаның шыңы
\(\displaystyle y=k(x-a)^2+b{ \small ,}\) теңдеуімен берілген параболаның шыңы \(\displaystyle (a;\,b){\small}\) координаталары бар нүкте.
Сондықтан \(\displaystyle y=3(x-1)^2+1\) функциясының графигін құру үшін параболаның \(\displaystyle O\) шыңын \(\displaystyle y=3x^2\) параболаның \(\displaystyle y=3(x-1)^2+1{\small }\) шыңына жылжыту қажет.
\(\displaystyle y=3(x-1)^2+1{ \small,}\) теңдеуімен берілген параболаның шыңында координаттар бар \(\displaystyle (1;\,1){\small .}\)

Содан кейін \(\displaystyle B\) нүктесінің координаттары болады\(\displaystyle (2;\, -2){\small .}\)