Двигая точку \(\displaystyle A\) по графику квадратичной функции \(\displaystyle y=-(x-a)^2-b{ \small ,}\) найдите параметры \(\displaystyle a,\, b\) (с точностью до десятых) и запишите уравнение параболы.
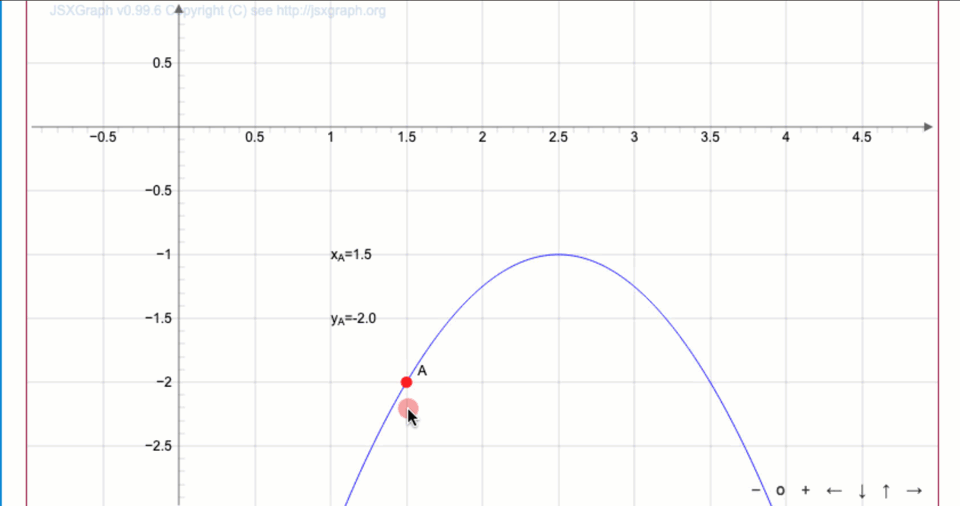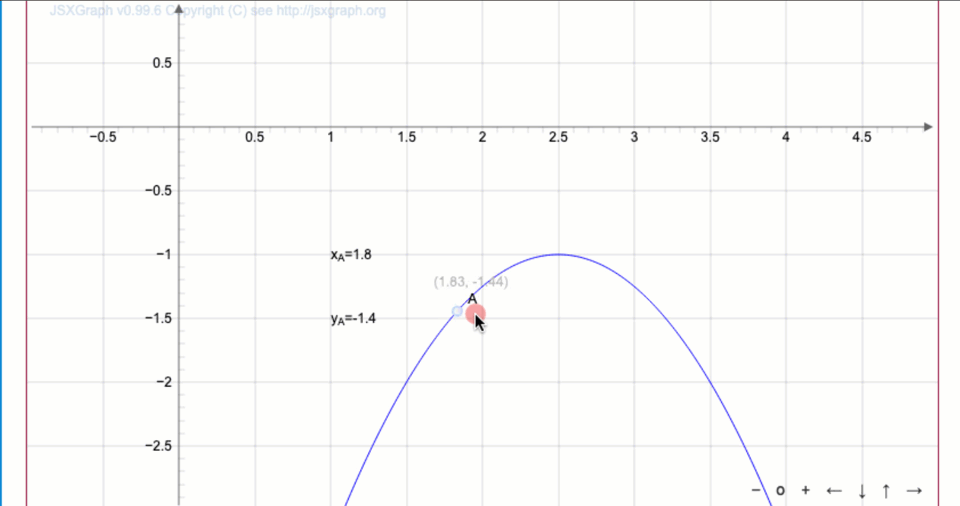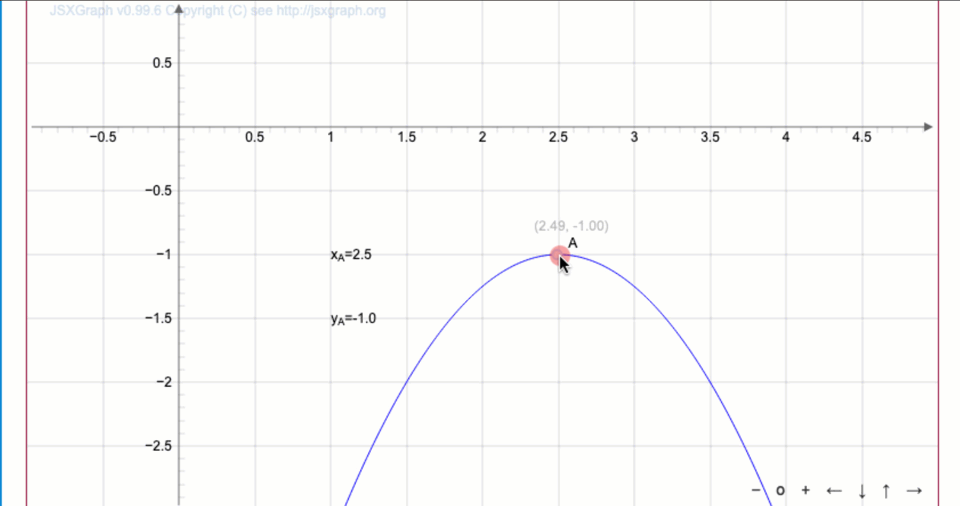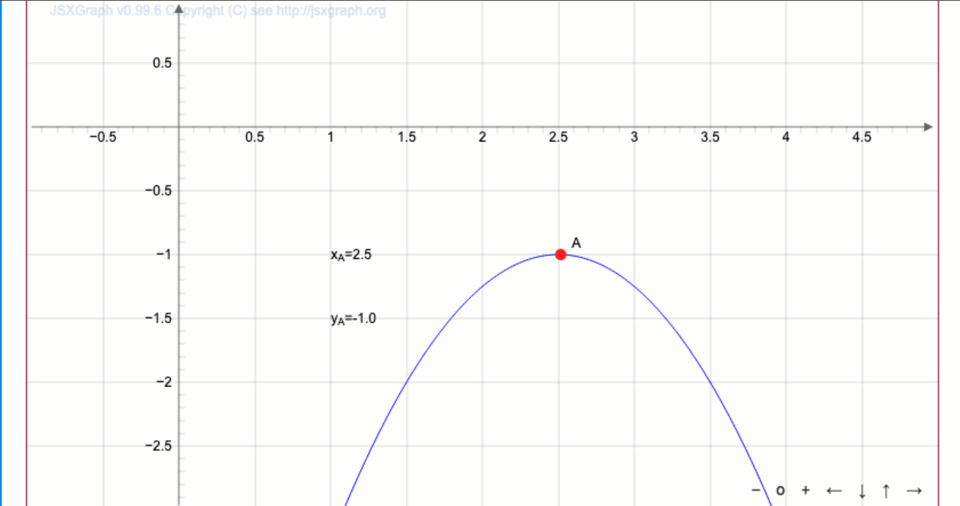
Запишите уравнение параболы:
\(\displaystyle y=-(x-\)\(\displaystyle )^2-\)
Вершина параболы, заданной уравнением \(\displaystyle y=k(x-a)^2+b\)
Вершиной параболы, заданной уравнением \(\displaystyle y=k(x-a)^2+b{ \small ,}\) называется точка с координатами \(\displaystyle (a;\,b){\small.}\)
График функции \(\displaystyle y=k(x-a)^2+b\) получен из графика параболы \(\displaystyle y=kx^2\)
- сдвигом каждой точки на \(\displaystyle a\) единиц вправо вдоль оси \(\displaystyle \rm OX{\small ,}\)
- сдвигом каждой точки на \(\displaystyle b\) единиц вверх вдоль оси \(\displaystyle \rm OY{\small .}\)
Тогда вершина параболы \(\displaystyle y=kx^2\) точка \(\displaystyle (0;\,0)\) перейдёт в точку \(\displaystyle (0+a;0+b)=(a;\,b){\small .}\)
Из графика функции
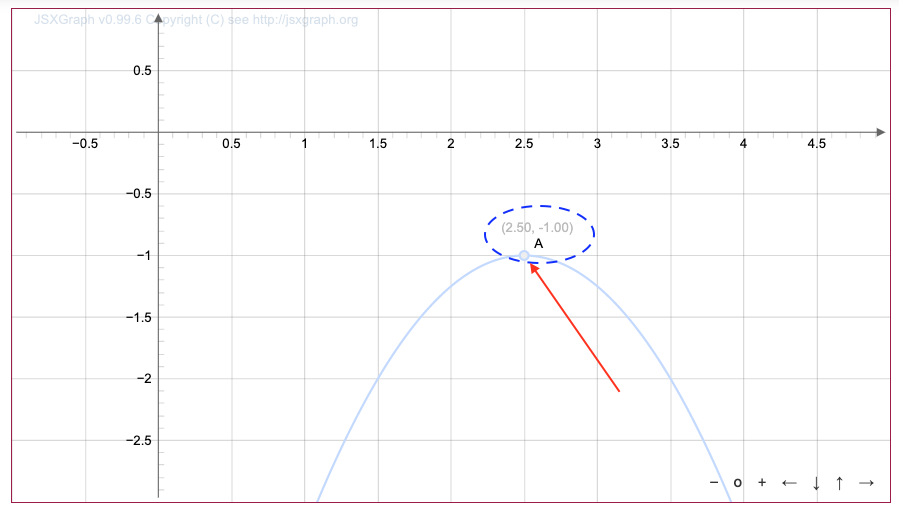
следует, что вершина имеет координаты \(\displaystyle (2{,}5;\, -1)\)
Тогда данный график задан уравнением \(\displaystyle y=\color{red}{k}(x-3)^2+1\) для некоторого коэффиента \(\displaystyle \color{red}{k}{\small .}\)
По условию был дан график функции \(\displaystyle y=\color{red}{-}(x-a)^2+b{\small .}\)
Следовательно, \(\displaystyle \color{red}{k}=\color{red}{-1}\) и данная парабола задана уравнением \(\displaystyle y=-(x-3)^2+1{\small .}\)