\(\displaystyle A\) нүктесін квадраттық функцияның графигі бойымен жылжыту \(\displaystyle y=-(x-a)^2-b{ \small ,}\) \(\displaystyle a,\, b\) (ондық бөлігіне дейін) параметрлерін тауып, параболаның теңдеуін жазыңыз.
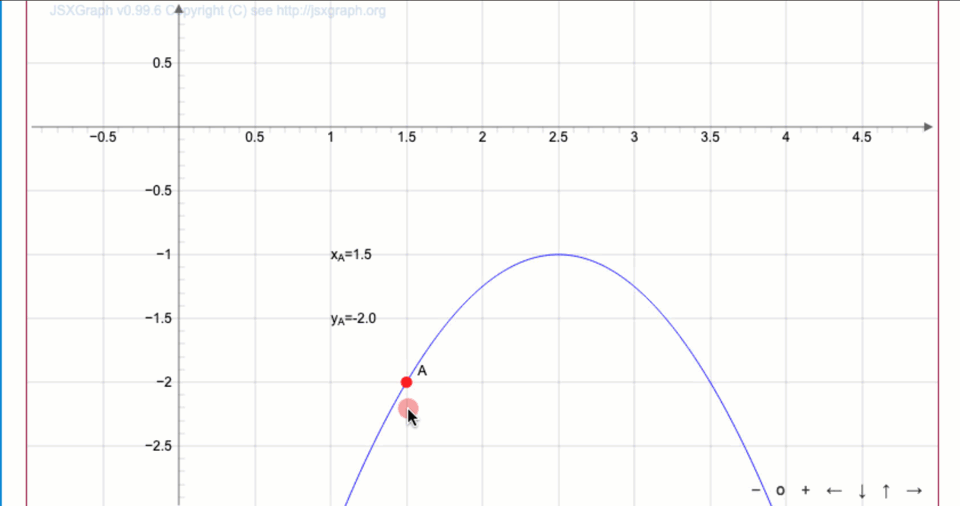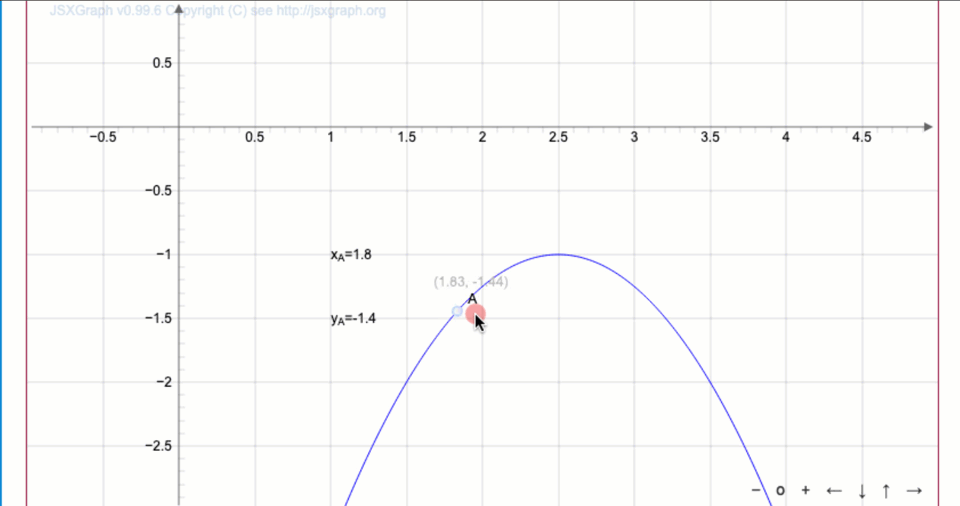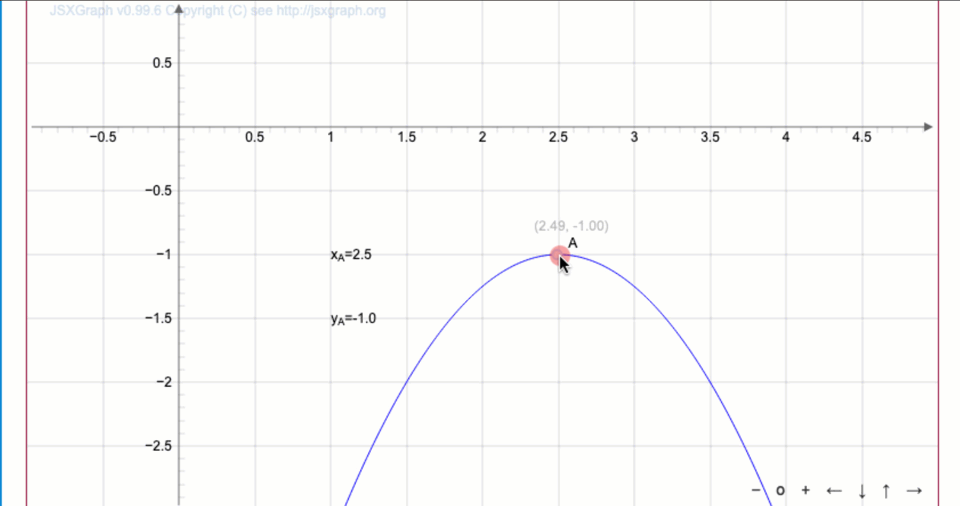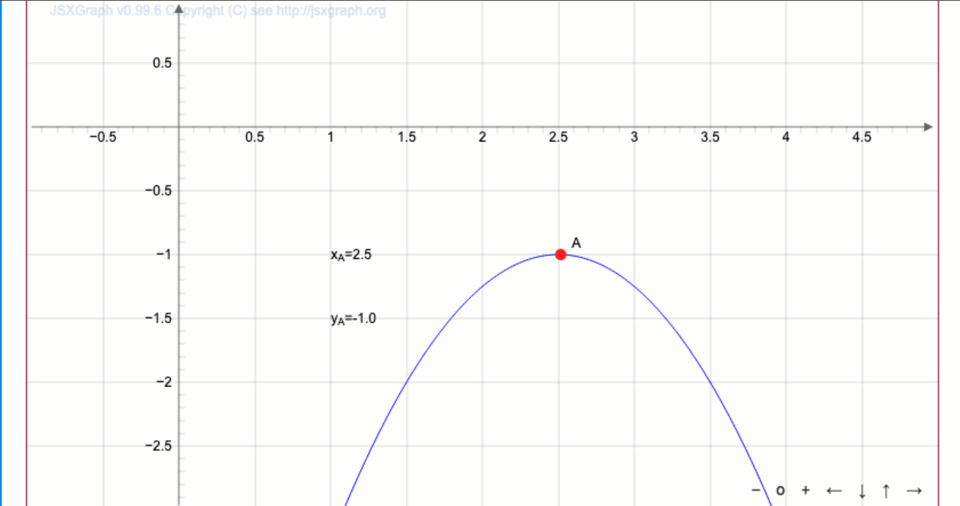
Парабола теңдеуін жазыңыз:
\(\displaystyle y=-(x-\)\(\displaystyle )^2-\)
\(\displaystyle y=k(x-a)^2+b\) теңдеуімен берілген параболаның шыңы
\(\displaystyle y=k(x-a)^2+b{ \small ,}\) теңдеуімен берілген параболаның шыңы \(\displaystyle (a;\,b){\small.}\) координаталары бар нүкте.
Функция графигі \(\displaystyle y=k(x-a)^2+b\) парабола \(\displaystyle y=kx^2\) графигінен алынған
- әрбір \(\displaystyle a\) нүктені ось бойымен \(\displaystyle \rm OX{\small }\) бірлікке оңға жылжыту,
- әрбір \(\displaystyle b\) нүктені ось бойымен \(\displaystyle \rm OY{\small }\) бірлікке жылжыту.
Сонда параболаның шыңы \(\displaystyle y=kx^2\) \(\displaystyle (0;\,0)\) нүктесі \(\displaystyle (0+a;0+b)=(a;\,b){\small }\) нүктесіне шығады.
Функция графигінен
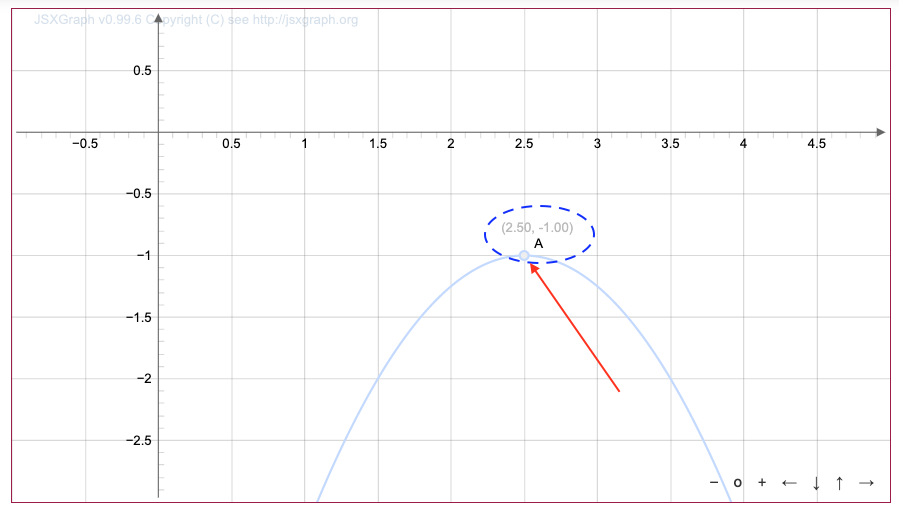
төбенің координаталары \(\displaystyle (2{,}5;\, -1)\) болатыны шығады.
Сонда бұл график кейбір коэффициент \(\displaystyle \color{red}{k}{\small }\) үшін\(\displaystyle y=\color{red}{k}(x-3)^2+1\) теңдеуімен беріледі.
Шарт бойынша \(\displaystyle y=\color{red}{-}(x-a)^2+b{\small }\) функция графигі берілген
Демек, \(\displaystyle \color{red}{k}=\color{red}{-1}\) және бұл парабола \(\displaystyle y=-(x-3)^2+1{\small }\) теңдеуімен берілген.