Тік бұрышты үшбұрышта \(\displaystyle ABC\) бұрыш \(\displaystyle C\) түзу, \(\displaystyle \angle B=58^{\circ},\) \(\displaystyle CD-\) медиана. \(\displaystyle \angle ACD{\small }\) табыңыз
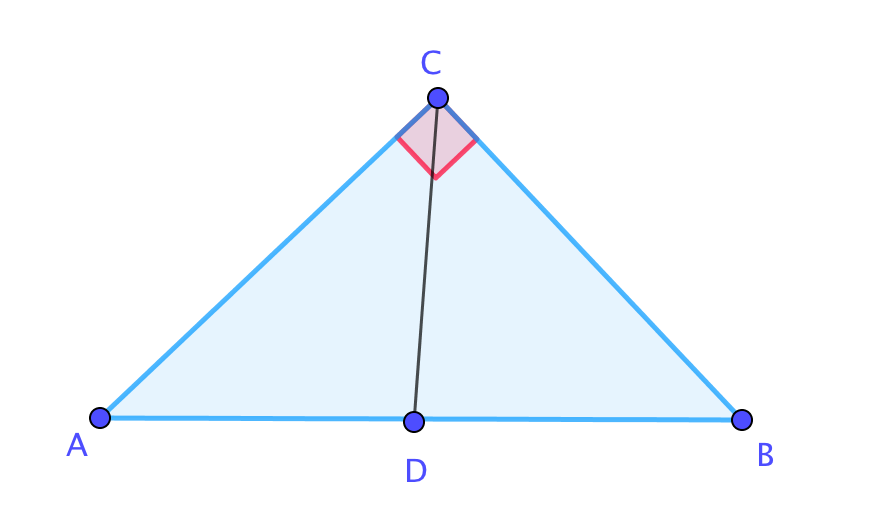
Гипотенузаға жүргізілген медиана гипотенузаның жартысына тең, яғни \(\displaystyle AD=CD=BD{\small . } \) Біз \(\displaystyle CDB \) және \(\displaystyle ACD \) үшбұрыштар теңбүйірлі екенін аламыз.
Демек,
\(\displaystyle \angle DCB= \angle CBD= 58^\circ{\small ,}\)
\(\displaystyle \angle ACD= \angle CAD{\small . } \)
\(\displaystyle C \) бұрыш \(\displaystyle 90^\circ \) тең және \(\displaystyle \angle ACD+ \angle DCB{\small }\) тең. Сондықтан
\(\displaystyle 90^\circ= \angle ACD+ \angle DCB{\small , } \)
\(\displaystyle 90^\circ= \angle ACD+ 58^\circ{\small , } \)
\(\displaystyle \angle ACD= 90^\circ- 58^\circ{\small , } \)
\(\displaystyle \angle ACD= 32^\circ{\small . } \)
Демек,
\(\displaystyle \angle A= \angle CAD= \angle ACD= 32^\circ{\small .} \)
Жауап: \(\displaystyle 32 {\small .} \)