\(\displaystyle ABC\) үшбұрыштағы \(\displaystyle AC\) және \(\displaystyle BC\) жақтар тең. \(\displaystyle B\) шыңындағы сыртқы бұрыш \(\displaystyle 138^{\circ}{\small }\) тең
Бұрышты \(\displaystyle \angle C{\small }\) табыңыз
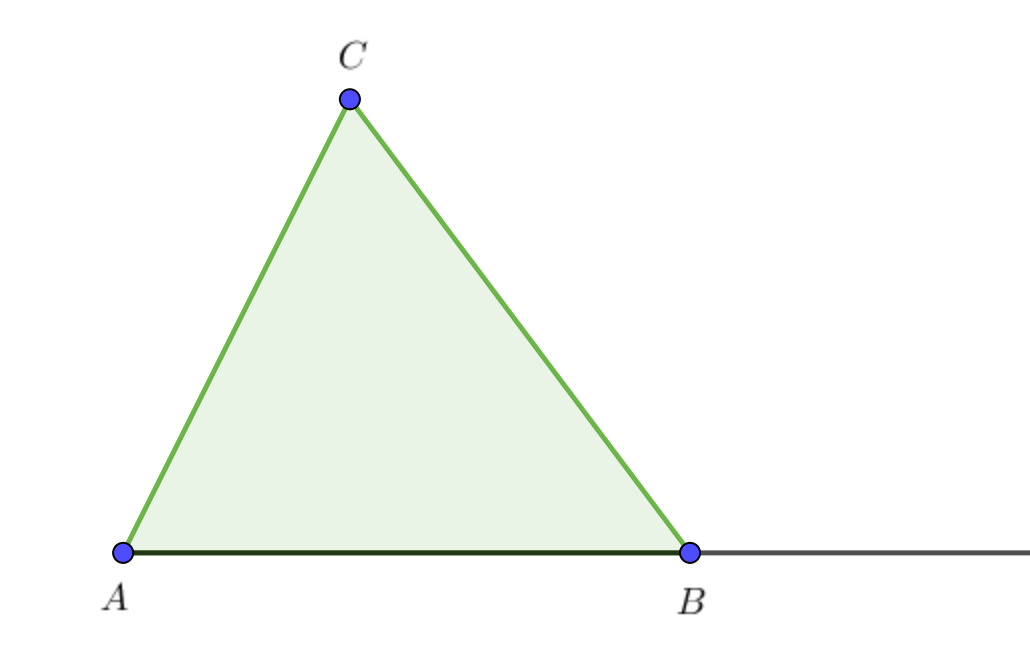
Жоғарғы жағындағы сыртқы бұрыш \(\displaystyle C \) оған іргелес емес екі ішкі бұрыштың қосындысына тең:
\(\displaystyle \angle A+ \angle C= 138^\circ{\small . } \)
Теңбүйірлі үшбұрышта негіздегі бұрыштар тең болады. Біздің жағдайда \(\displaystyle \angle A= \angle B{\small . } \) Осыдан,
\(\displaystyle \angle A+ \angle B+ \angle C=180^\circ{\small , } \)
\(\displaystyle \angle A+ \angle A+ \angle C=180^\circ{\small , } \)
аламыз
\(\displaystyle 2\angle A+ \angle C=180^\circ{\small . } \)
Онда жүйені аламыз:
\(\displaystyle \left\{\begin{aligned}2\angle A+ \angle C&=180^\circ{\small , }\\\angle A+ \angle C&= 138^\circ{\small .}\end{aligned}\right. \)
Бірінші теңдеуден \(\displaystyle \angle C= 180^\circ- 2\angle A{\small . } \)Екіншіге қоя отырып, аламыз:
\(\displaystyle \angle A+ 180^\circ- 2\angle A= 138^\circ{\small , } \)
\(\displaystyle -\angle A= 138^\circ- 180^\circ{\small , } \)
\(\displaystyle -\angle A= -42^\circ{\small , } \)
\(\displaystyle \angle A= 42^\circ{\small . } \)
Осылайша,
\(\displaystyle \angle C= 180^\circ- 2\angle A{\small , } \)
\(\displaystyle \angle C= 180^\circ- 2\cdot 42^\circ{\small , } \)
\(\displaystyle \angle C= 180^\circ- 84^\circ{\small , } \)
\(\displaystyle \angle C= 96^\circ {\small.}\)
Жауап: \(\displaystyle 96 {\small . } \)