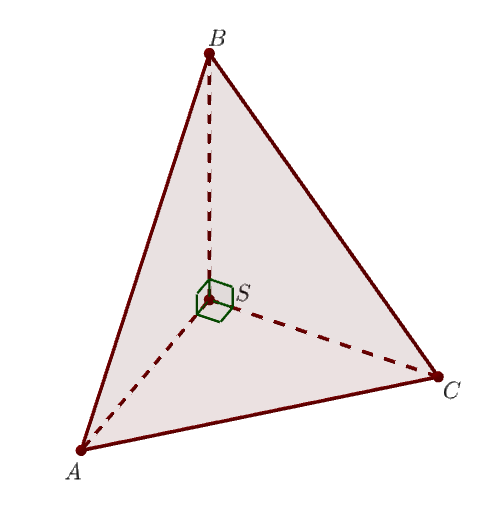
Үшбұрышты пирамиданың бүйір қырлары өзара перпендикуляр, олардың әрқайсысы \(\displaystyle 3{\small }\) тең Пирамиданың көлемін табыңыз..
\(\displaystyle ABC\) – пирамиданың табаны, \(\displaystyle S\) – төбесі болсын.
1. Шарт бойынша:
- бүйір қабырғалары өзара перпендикуляр, яғни \(\displaystyle SA\perp SB{\small ,}\) \(\displaystyle SB\perp SC{\small ,}\) \(\displaystyle SA\perp SC{\small ;}\)
- бүйір қабырғалары \(\displaystyle 3{ \small ,} \) тең, яғни \(\displaystyle SA=SB=SC=3{\small .}\)
2. \(\displaystyle V=\frac{1}{3}S_{табан} \cdot h \) формуласы бойынша пирамиданың көлемін есептеу үшін табан ауданы мен биіктігін білу қажет.
Бұл жағдайда:
|  |
Осылайша, пирамиданың биіктігі
\(\displaystyle h=SB=3{\small }\) тең.
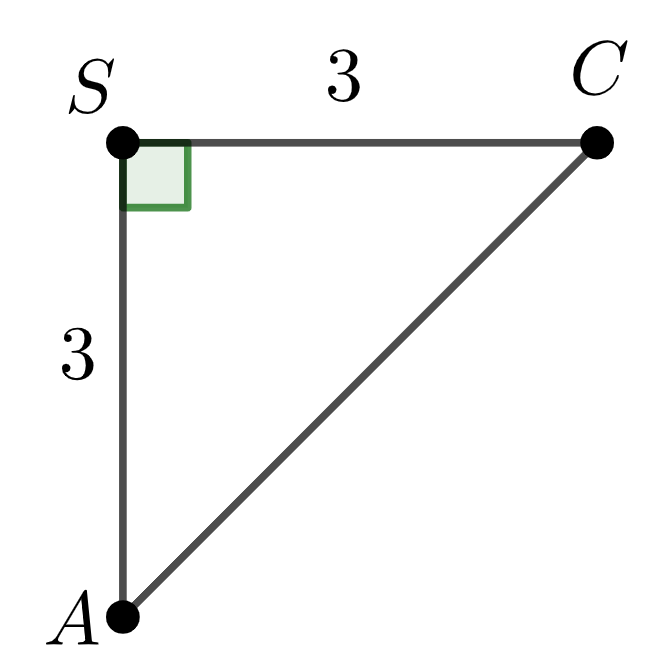
\(\displaystyle SAC \) табанының ауданы келесіге тең
Пирамида көлемінің формуласына \(\displaystyle h \) және \(\displaystyle S_{табан} \) алмастырайық:
\(\displaystyle V=\frac{1}{3}S_{табан} \cdot h=\frac{1}{3}\cdot S_{\triangle SAC} \cdot SB = \frac{1}{3}\cdot \frac{9}{2}\cdot 3= 4{,}5{\small .}\)
Жауабы: \(\displaystyle 4{,}5{\small .}\)
\(\displaystyle SB \) қабырғасының \(\displaystyle SAC \) жазықтығына перпендикуляр екенін нақты дәлелдеу үшін түзу мен жазықтықтың перпендикулярлық белгісін қолданамыз.
Түзу мен жазықтықтың перпендикулярлық белгісі
Егер түзу бір жазықтықта жатқан екі қиылысатын түзуге перпендикуляр болса, онда ол сол жазықтыққа перпендикуляр болады.
Шарт бойынша \(\displaystyle SB\perp SA\) және \(\displaystyle SB\perp SC{\small .}\)
\(\displaystyle SA\) және \(\displaystyle SC\) түзулері \(\displaystyle S\) нүктесінде қиылысады және \(\displaystyle SAC \) жазықтығында жатады
Демек, \(\displaystyle SB \) \(\displaystyle SAC \) жазықтығына перпендикуляр