\(\displaystyle x^2-8x+13=0\) квадрат теңдеуі үшін дискриминантты есептеңіз
\(\displaystyle {\rm D}=\),
теңдеудің түбірлерін тауып, оларды ықшамдаңыз.
| \(\displaystyle x_1=\) | \(\displaystyle -\Big(\)\(\displaystyle \Big)+\)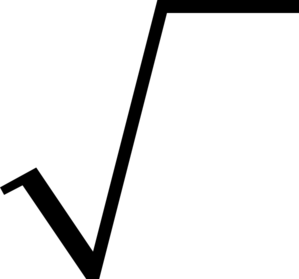 | \(\displaystyle =\) |
| \(\displaystyle x_2=\) | \(\displaystyle -\Big(\)\(\displaystyle \Big)-\)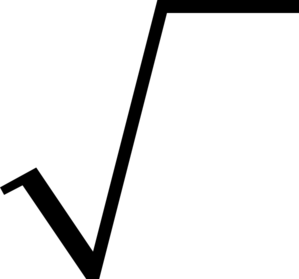 | \(\displaystyle =\) |
Ережені қолданайық
\(\displaystyle \color{blue}{ a}X^2+\color{green}{ b}X+\color{red}{ c}=0\) \(\displaystyle {\rm D}=\color{green}{ b}^2-4\color{blue}{ a}\color{red}{ c}\) \(\displaystyle x_1=\frac{-\color{green}{ b}+\sqrt{\rm D}}{2\color{blue}{ a}}\) \(\displaystyle x_1=\frac{-\color{green}{ b}-\sqrt{\rm D}}{2\color{blue}{ a}}\)Квадрат теңдеудің түбірі
теңдеуді оның коэффициенттерін бөліп алу арқылы жазайық:
\(\displaystyle x^2-8x+13=\color{blue}{ 1}\cdot x^2\color{green}{ -8}x+\color{red}{ 13}{\small . }\)
Сонда \(\displaystyle \color{blue}{ a}=\color{blue}{ 1}, \color{green}{ b}=\color{green}{ -8}, \color{red}{ c}=\color{red}{ 13}{\small .} \)
Дискриминантты есептеу үшін формуланы қолданайық:
\(\displaystyle {\rm D}=\color{green}{ b}^2-4\color{blue}{ a}\color{red}{ c}{\small .}\)
Сондықтан
\(\displaystyle {\rm D}= (\color{green}{ -8})^2-4\cdot \color{blue}{ 1}\cdot \color{red}{ 13}=64-52=12\)
және
\(\displaystyle \sqrt{\rm D}=\sqrt{ 12}=\sqrt{ 4\cdot 3}=2\sqrt{ 3} {\small .} \)
Демек, теңдеудің түбірлері мыналарға тең
\(\displaystyle x_1=\frac{-(-8)+\sqrt{12}}{2}=\frac{8+2\sqrt{3} }{ 2 }=4+\sqrt{ 3}{\small ,}\)
\(\displaystyle x_2=\frac{-(-8)-\sqrt{12}}{2}=\frac{8-2\sqrt{3} }{ 2 }=4-\sqrt{ 3}{\small .}\)
Жауабы: \(\displaystyle {\rm D}=12{ \small ,}\, x_1=\frac{-(-8)+\sqrt{12}}{2}=4+\sqrt{ 3}{\small ,} \, x_2=\frac{-(-8)-\sqrt{12}}{2}=4-\sqrt{ 3}{\small .} \)