\(\displaystyle AD\) және \(\displaystyle BC\) түзулері \(\displaystyle O\) нүктесінде қиылысады . Егер \(\displaystyle ∠ AOB=150^{\circ}\) екені белгілі болса , \(\displaystyle BOD\), \(\displaystyle COD\) және \(\displaystyle AOC\) бұрыштарының мәндерін табыңыз.
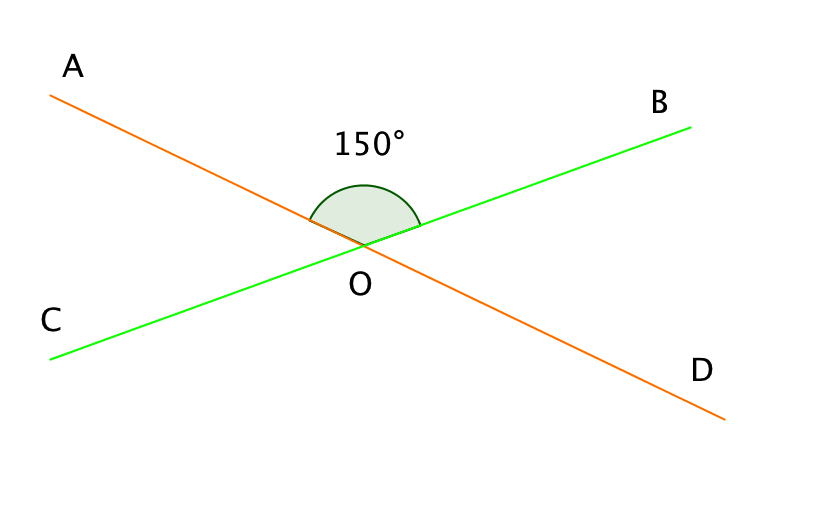
\(\displaystyle ∠ BOD=\) \(\displaystyle ^{\circ}\)
\(\displaystyle ∠ COD=\) \(\displaystyle ^{\circ}\)
\(\displaystyle ∠ AOC=\) \(\displaystyle ^{\circ}\)
Іргелес және тік бұрыштар. Іргелес және тік бұрыштардың қасиеттері
\(\displaystyle ABC\) жазыңқы бұрышының ішінде \(\displaystyle BD\) сәулесі жүргізілген. Ол жазыңқы бұрышты іргелес бұрыштар деп аталатын екі бұрыш - \(\displaystyle ∠ ABD\) және \(\displaystyle ∠ DBC\)бөледі.
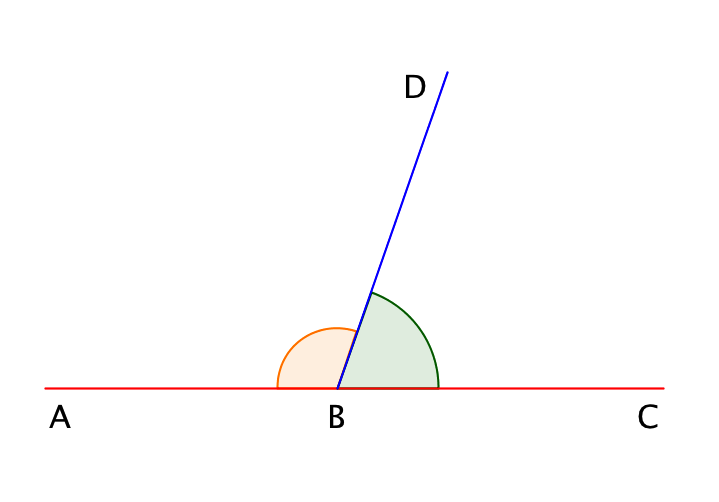
Іргелес бұрыштардың қосындысы \(\displaystyle 180\) градусқа тең:
\(\displaystyle ∠ ABD+∠ DBC=180^{\circ}.\)
Егер екі \(\displaystyle AB\) және \(\displaystyle CD\) түзулері \(\displaystyle O\) нүктесінде қиылысса, онда \(\displaystyle AOC\) және \(\displaystyle BOD\) бұрыштары тік деп аталады. Тік бұрыштардың басқа жұбы \(\displaystyle AOD\) және \(\displaystyle BOC\) бұрыштары болып табылады:
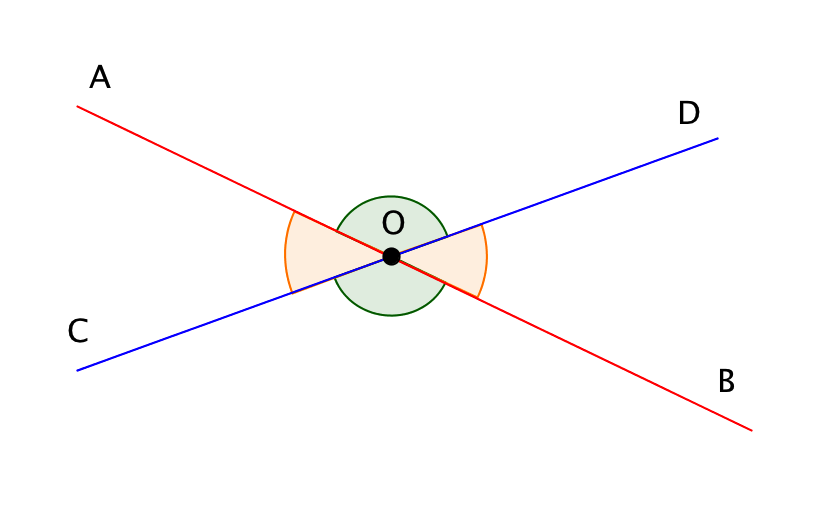
Тік бұрыштар келесіге тең:
\(\displaystyle ∠ AOC=∠ BOD,\)
\(\displaystyle ∠ AOD=∠ BOC.\)
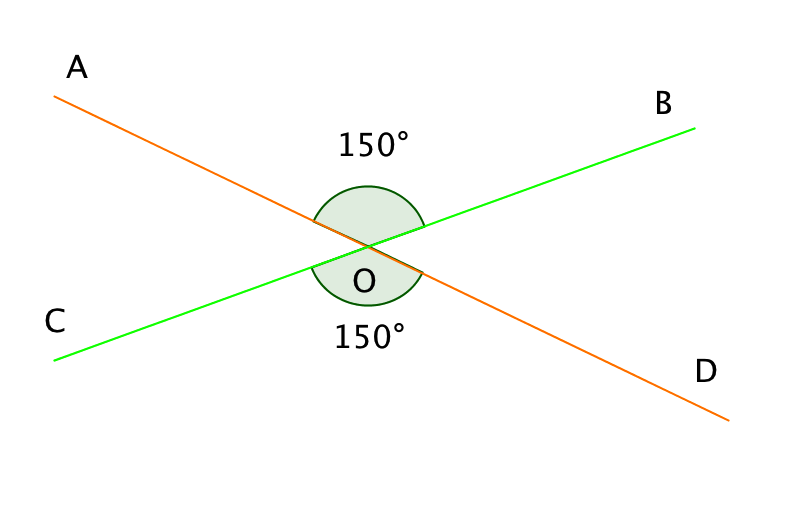
\(\displaystyle AOB\) және \(\displaystyle BOD\) бұрыштары іргелес болғандықтан, онда \(\displaystyle ∠ AOB+∠ BOD=180^{\circ}.\)
Демек,
\(\displaystyle ∠ BOD=180^{\circ} -∠ AOB=180^{\circ} - 150^{\circ}=30^{\circ}.\)
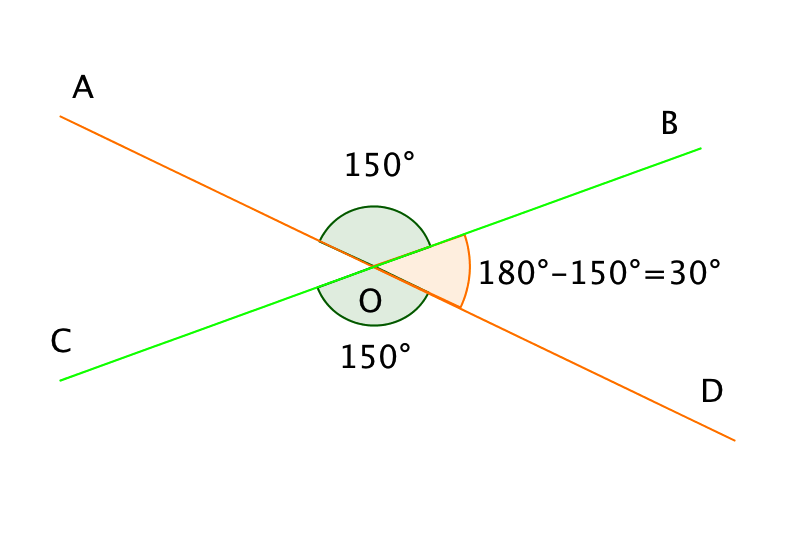
\(\displaystyle BOD\) және \(\displaystyle AOC\) бұрыштары тік болғандықтан, онда \(\displaystyle ∠ AOC=∠ BOD=30^{\circ}.\)
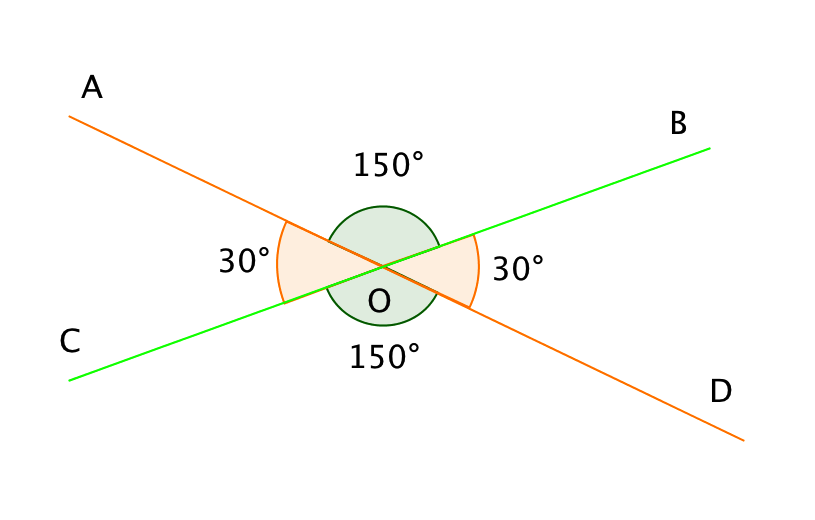
Жауабы: \(\displaystyle ∠ BOD=30^{\circ}, ∠ COD=150^{\circ}, ∠ AOC=30^{\circ}.\)