Найдите вероятность попадания из точки \(\displaystyle A\) в точку \(\displaystyle G{ \small ,}\) если на каждой развилке путь выбирается наудачу (то есть на каждой развилке выборы равноправны) и движение происходит только по направлению стрелок.
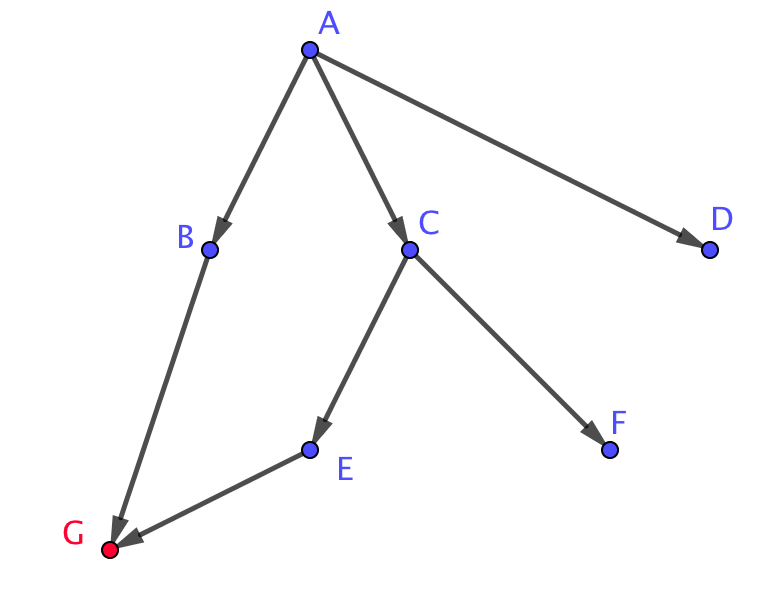
Из пункта \(\displaystyle А\) попасть в пункт \(\displaystyle G\) можно двумя путями:
| \(\displaystyle A \rightarrow B \rightarrow G\) | \(\displaystyle A \rightarrow С \rightarrow Е \rightarrow G\) |
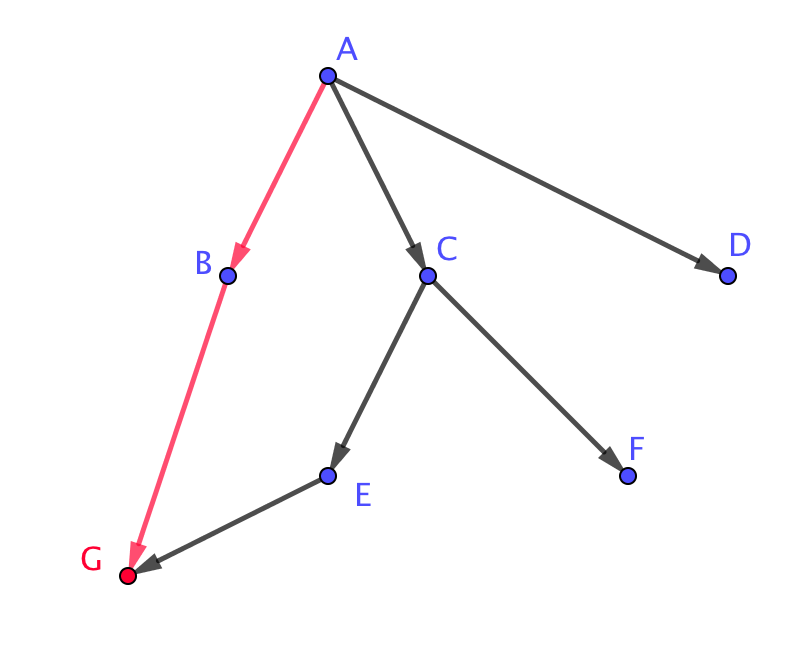 | 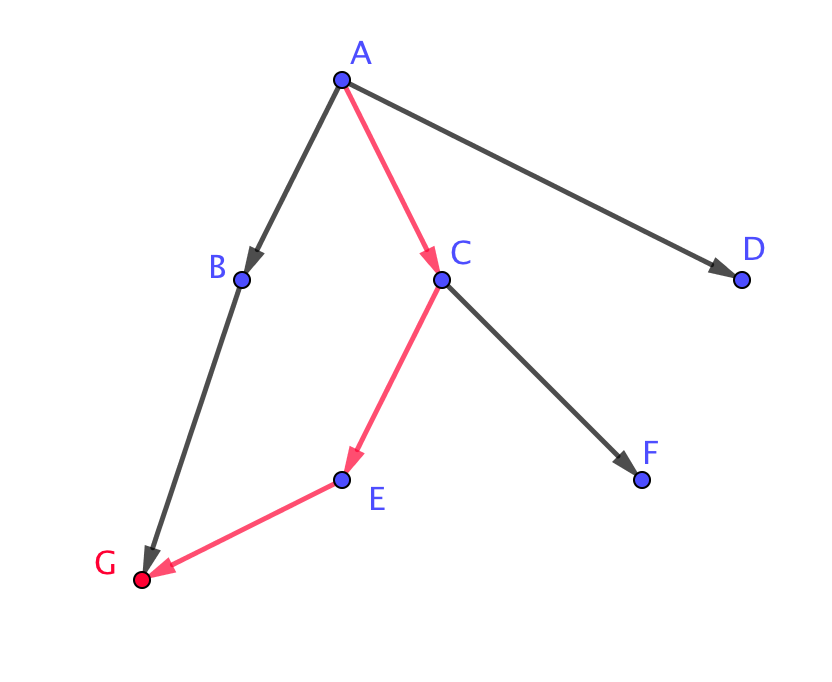 |
Так как данные события несовместны (нельзя пройти по двум путям сразу), то
\(\displaystyle P(AG)=P(ABG)+P(ACEG){\small .}\)
Найдем вероятность прохождения каждого из данных маршрутов:
- Вероятность попадания в точку \(\displaystyle B\) из точки \(\displaystyle A\) равна \(\displaystyle \frac{1}{3}{ \small ,}\) так как из точки \(\displaystyle A\) выходят три пути.
- Вероятность попадания в точку \(\displaystyle G\) из точки \(\displaystyle B\) равна \(\displaystyle 1{ \small ,}\) так как из точки \(\displaystyle B\) есть только один путь.
Поэтому \(\displaystyle P(ABG)=\frac{1}{3}\cdot 1=\frac{1}{3}{\small .}\)
- Вероятность попадания в точку \(\displaystyle C\) из точки \(\displaystyle A\) равна \(\displaystyle \frac{1}{3}{ \small ,}\) так как из точки \(\displaystyle A\) выходят три пути.
- Вероятность попадания в точку \(\displaystyle E\) из точки \(\displaystyle C\) равна \(\displaystyle \frac{1}{2}{ \small ,}\) так как из точки \(\displaystyle C\) выходят два пути.
- Вероятность попадания в точку \(\displaystyle G\) из точки \(\displaystyle C\) равна \(\displaystyle 1{ \small ,}\) так как из точки \(\displaystyle C\) есть только один путь.
Поэтому \(\displaystyle P(ACEG)=\frac{1}{3}\cdot \frac{1}{2}\cdot 1=\frac{1}{6}{\small .}\)
Таким образом, вероятность попадания в точку \(\displaystyle G\) из точки \(\displaystyle A\) равна
\(\displaystyle P(AG)=P(ABG)+P(ACEG)=\frac{1}{3}+\frac{1}{6}=\frac{3}{6}=0{,}5{\small .}\)
Ответ:\(\displaystyle 0{,}5{\small .}\)