Вероятность попадания точки во множество \(\displaystyle \rm A\) равна \(\displaystyle 0{,}7{\small , }\) вероятность попадания точки во множество \(\displaystyle \rm B\) равна \(\displaystyle 0{,}8{ \small ,}\) а вероятность попадания точки в \(\displaystyle A \cap B\) равна \(\displaystyle 0{,}56{\small . }\)
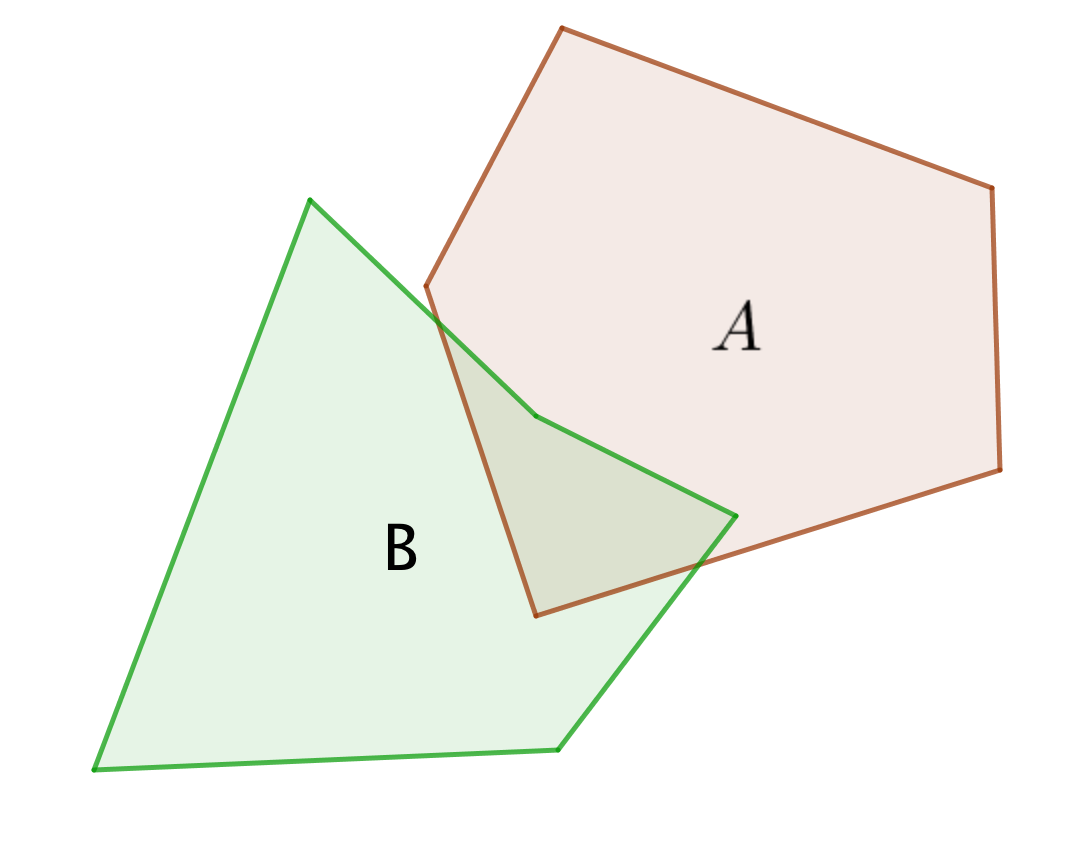
Найдите вероятность, что точка попадет во множество \(\displaystyle \rm A\) или во множество \(\displaystyle \rm B{\small .}\)
Вероятность попадания точки во множество \(\displaystyle \rm A\) равна \(\displaystyle 0{,}7{\small , }\) а вероятность попадания точки во множество \(\displaystyle \rm B\) равна \(\displaystyle 0{,}8{\small . }\) Также известно, что данные события независимы.

Так как площадь фигуры \(\displaystyle A \cup B\) равна сумме площадей фигур \(\displaystyle A\) и \(\displaystyle B\) минус \(\displaystyle A\cap B\) (так как пересечение входит в оба множества и при суммировании считается дважды), то
\(\displaystyle P(A \cup B)=P(A)+P(B)-P(A\cap B)\)
или
\(\displaystyle P(A + B)=P(A)+P(B)-P(A\cdot B){\small .}\)
Таким образом,
\(\displaystyle P(A + B)=0{,}7+0{,}8-0{,}56=0{,}94{\small .}\)
Ответ:\(\displaystyle 0{,}94{\small .}\)