Автомат выбирает случайную точку из квадрата со стороной длины \(\displaystyle 1{\small .}\) Найдите вероятность того, что эта точка принадлежит вписанному в данный квадрат кругу с диаметром \(\displaystyle 1{\small .}\)
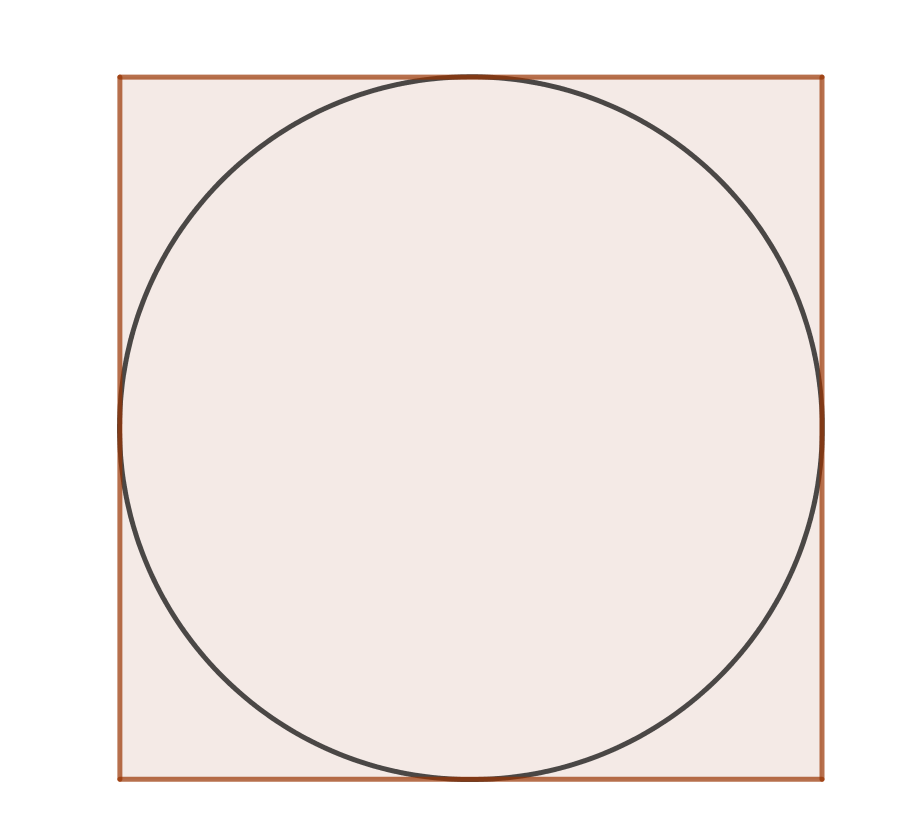
Геометрическое определение вероятности на плоскости
На плоскости отмечена синяя область \(\displaystyle F\small,\) внутри которой отмечена красная область \(\displaystyle G\small.\)
Тогда вероятность того, что случайная точка области \(\displaystyle F\) окажется в области \(\displaystyle G\small,\) равна
\(\displaystyle \frac{\small{площадь}\,\,\color{red}{G}}{\small{площадь}\,\,\color{blue}{F}}\)
В нашем случае мы ищем вероятность того, что точка из квадрата попадет во вписанную в этот квадрат окружность.
Площадь квадрата со стороной \(\displaystyle 1\) равна
\(\displaystyle 1^2=1{\small .}\)
Площадь круга с диаметром \(\displaystyle 1\) ( радиуса \(\displaystyle 0{,}5\)) равна
\(\displaystyle \pi\cdot (0{,}5)^2=0{,}25\pi{\small .}\)
Таким образом, вероятность, что точка из квадрата принадлежит кругу, равна
\(\displaystyle \frac{0{,}25\pi}{1}=0{,}25\pi{\small .}\)
Ответ:\(\displaystyle 0{,}25\pi{\small .}\)