Построение графика функции \(\displaystyle y=2x^2+4x-1{\small .}\)
Найдите координаты вершины параболы, заданной уравнением \(\displaystyle y=2x^2+4x-1{\small .}\)
Найдите неизвестный коэффициент и перепишите уравнение параболы \(\displaystyle y=2x^2+4x-1\) в виде
Постройте по точкам график функции \(\displaystyle y=2x^2{\small :}\)
| \(\displaystyle x\) | \(\displaystyle -3\) | \(\displaystyle -2\) | \(\displaystyle -1\) | \(\displaystyle 0\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) |
| \(\displaystyle y\) |
Меняя ползунками значения параметров \(\displaystyle a\) и \(\displaystyle b{ \small ,}\) постройте график \(\displaystyle y=2 (x-(-1))^2 + (-3){\small .}\)
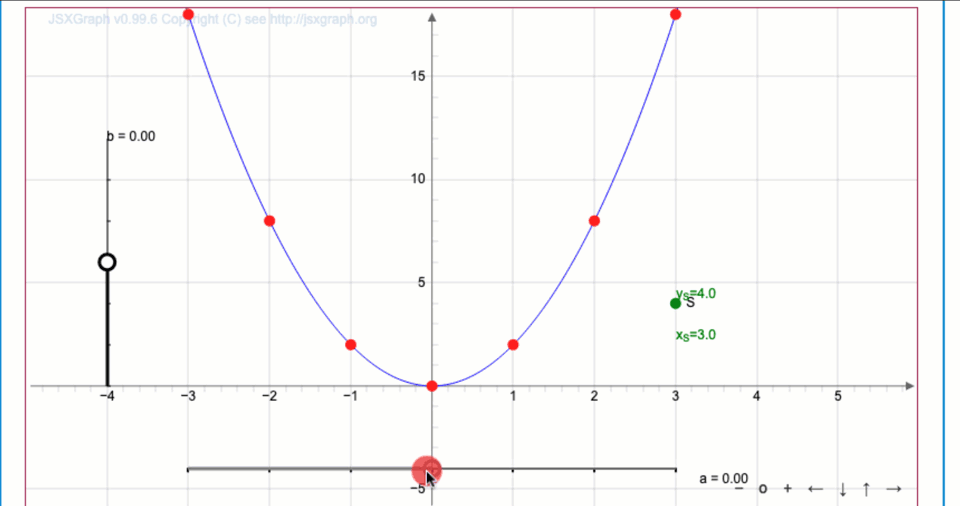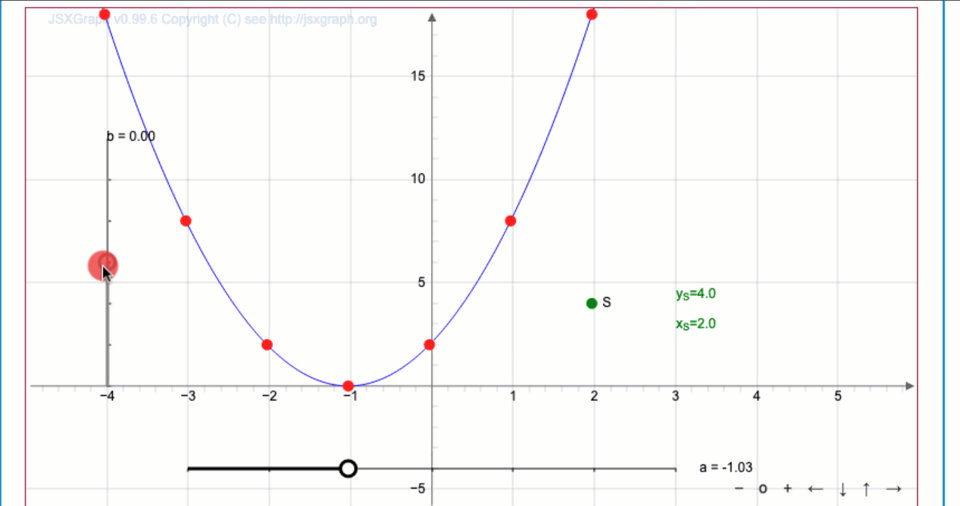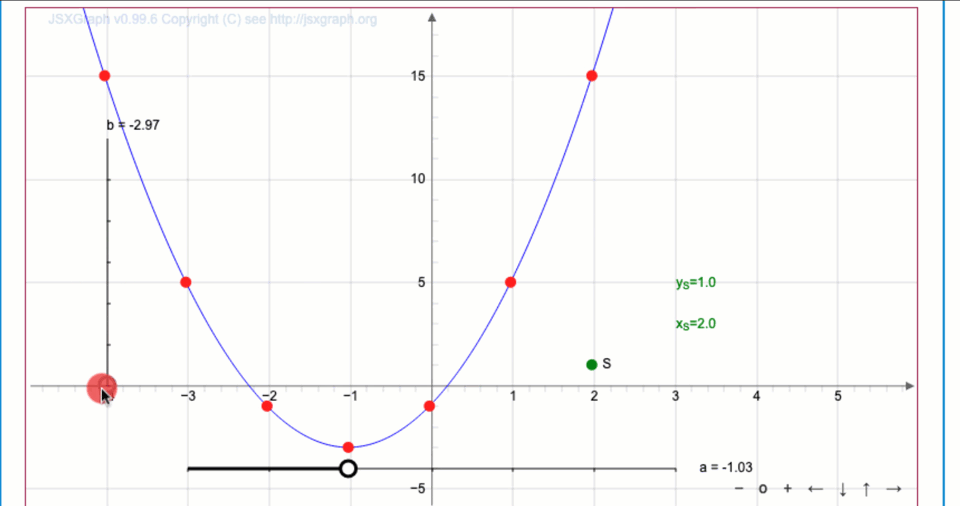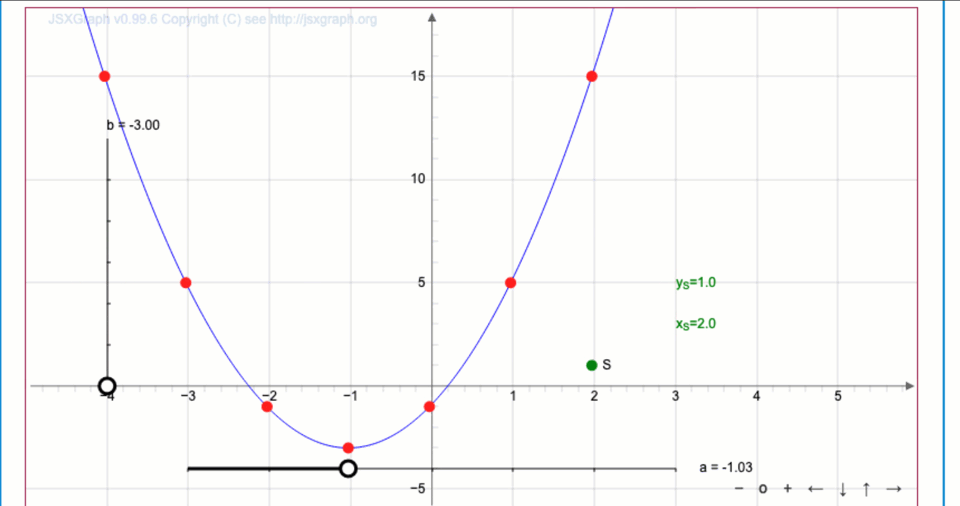
Координаты вершины параболы
Если парабола задана уравнением \(\displaystyle y=ax^2+bx+c{\small ,}\) то координаты вершины можно найти по формулам:
\(\displaystyle x_{0}=\frac{-b}{2a}\)
и
подставляя \(\displaystyle x_0\) в уравнение, можно найти \(\displaystyle y_0{\small .}\)
Для уравнения
\(\displaystyle y=2x^2+4x-1{\small .}\)
\(\displaystyle a=2,\, b=4\) и \(\displaystyle c=-1{\small .}\)
Тогда
\(\displaystyle x_0=-\frac{4}{2\cdot 2},\) то есть \(\displaystyle x_0=-1{\small .}\)
Подставляя \(\displaystyle x_0=-1\) в уравнение \(\displaystyle y=2x^2+4x-1{\small ,}\) получаем:
\(\displaystyle y_0=2\cdot (-1)^2+4\cdot (-1)-1{\small ,}\)
\(\displaystyle y_0=-3{\small .}\)
Напомним, что
Вершина параболы, заданной уравнением \(\displaystyle y=k(x-a)^2+b\)
Вершиной параболы, заданной уравнением \(\displaystyle y=k(x-a)^2+b{ \small ,}\) называется точка с координатами \(\displaystyle (a;\,b){\small.}\)
Мы нашли вершину: \(\displaystyle (-1;-3){\small .}\)
Тогда данный график задан уравнением \(\displaystyle y=\color{red}{k}(x+1)^2-3\) для некоторого коэффициента \(\displaystyle \color{red}{k}{\small .}\)
По условию был дан график функции \(\displaystyle y=\color{red}{2}x^2+4x-1{\small .}\)
Следовательно, \(\displaystyle \color{red}{k}=\color{red}{2}\) и данная парабола может быть задана уравнением
\(\displaystyle y=2(x+1)^2-3{\small .}\)
Заполним таблицу для функции \(\displaystyle y=2 x^2{\small :}\)
- \(\displaystyle x=-3{\small ,}\) тогда \(\displaystyle y=2\cdot (-3)^2{\small ,}\) следовательно \(\displaystyle y=18{\small ;}\)
- \(\displaystyle x=-2{\small ,}\) тогда \(\displaystyle y=2\cdot (-2)^2{\small ,}\) следовательно\(\displaystyle y=8{\small ;}\)
- \(\displaystyle x=-1{\small ,}\) тогда \(\displaystyle y=2\cdot (-1)^2{\small ,}\) следовательно \(\displaystyle y=2{\small ;}\)
- \(\displaystyle x=0{\small ,}\) тогда \(\displaystyle y=2\cdot 0^2{\small ,}\) следовательно \(\displaystyle y=0{\small ;}\)
- \(\displaystyle x=1{\small ,}\) тогда \(\displaystyle y=2\cdot 1^2{\small ,}\) следовательно \(\displaystyle y=2{\small ;}\)
- \(\displaystyle x=2{\small ,}\) тогда \(\displaystyle y=2\cdot 2^2{\small ,}\) следовательно \(\displaystyle y=8{\small ;}\)
- \(\displaystyle x=3{\small ,}\) тогда \(\displaystyle y=2\cdot 3^2{\small ,}\) следовательно \(\displaystyle y=18{\small.}\)
| \(\displaystyle x\) | \(\displaystyle -3\) | \(\displaystyle -2\) | \(\displaystyle -1\) | \(\displaystyle 0\) | \(\displaystyle 1\) | \(\displaystyle 2\) | \(\displaystyle 3\) |
| \(\displaystyle y\) | \(\displaystyle 18\) | \(\displaystyle 8\) | \(\displaystyle 2\) | \(\displaystyle 0\) | \(\displaystyle 2\) | \(\displaystyle 8\) | \(\displaystyle 18\) |
Чтобы получить \(\displaystyle y=2(x+1)^2-3\) из \(\displaystyle y=2 x^2{ \small ,}\) надо:
- сдвинуть график \(\displaystyle y=2x^2\) на одну единицу влево вдоль оси \(\displaystyle \rm OX{\small ,}\)
- сдвинуть вниз на три единицы вдоль оси \(\displaystyle \rm OY{\small .}\)
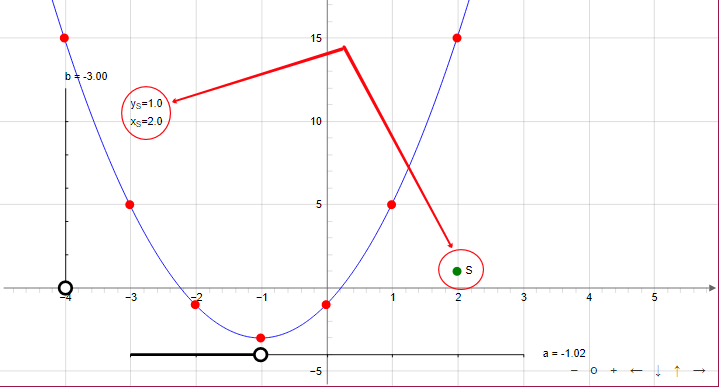
Тогда точка \(\displaystyle S \) имеет координаты \(\displaystyle (2;\,1){\small .}\)