Теория: Лекции по теме формулы сокращенного умножения (вторая степень)

Так как \(\displaystyle a\) и \(\displaystyle b\) – это положительные числа, то мы можем построить квадрат со стороной, равной \(\displaystyle a\) (например, сантиметров).

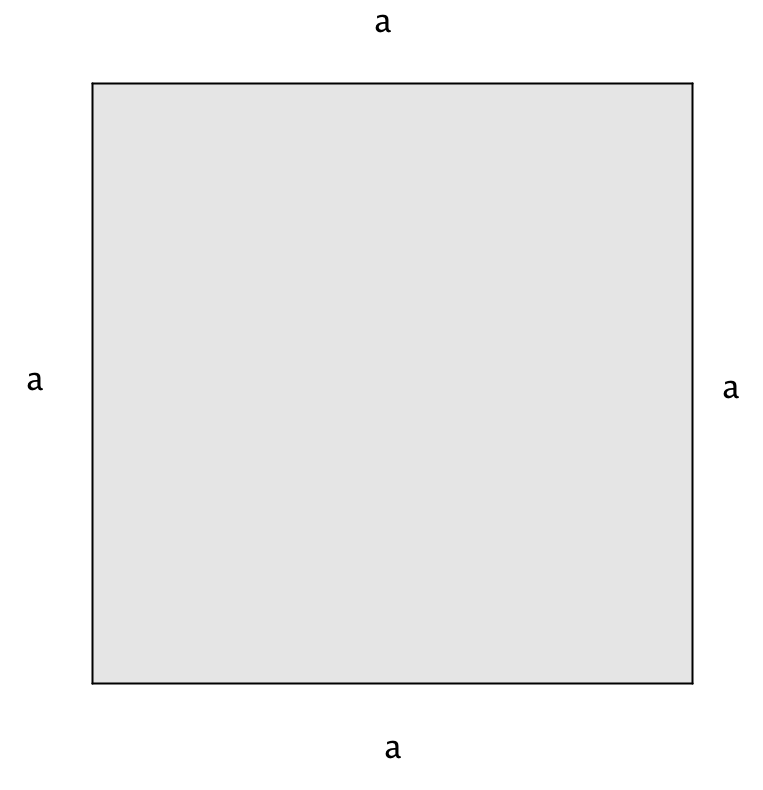
Площадь данного квадрата равна \(\displaystyle a^{\,2}\) (сантиметров квадратных).

Разобьем каждую сторону квадрата на две части длиной \(\displaystyle a-b\) и \(\displaystyle b\) так, как это показано на рисунке:

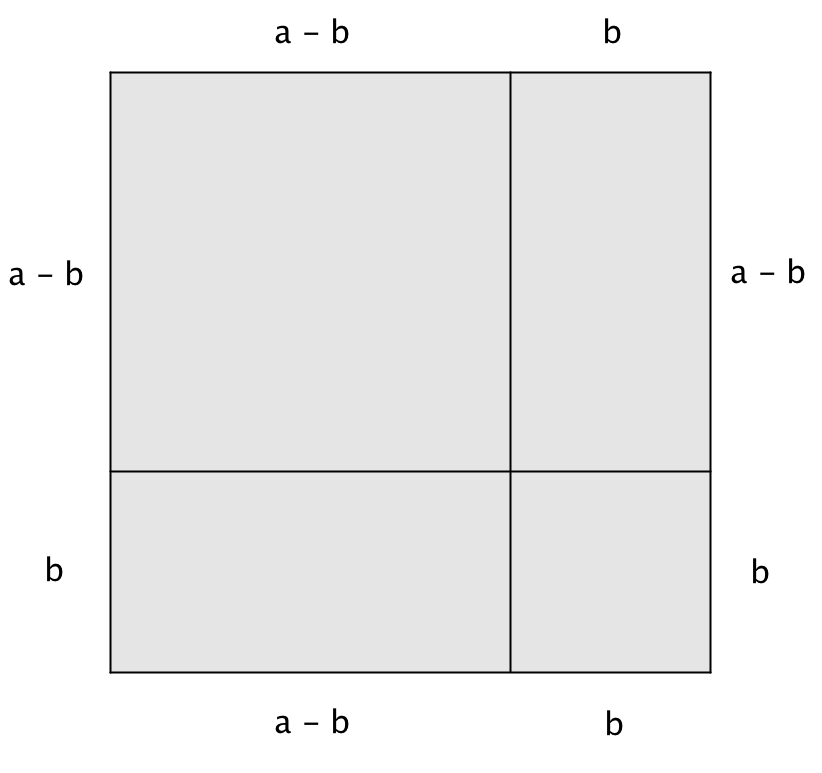
Квадрат со стороной \(\displaystyle a\) состоит из:

1) квадрата со стороной \(\displaystyle a - b,\)

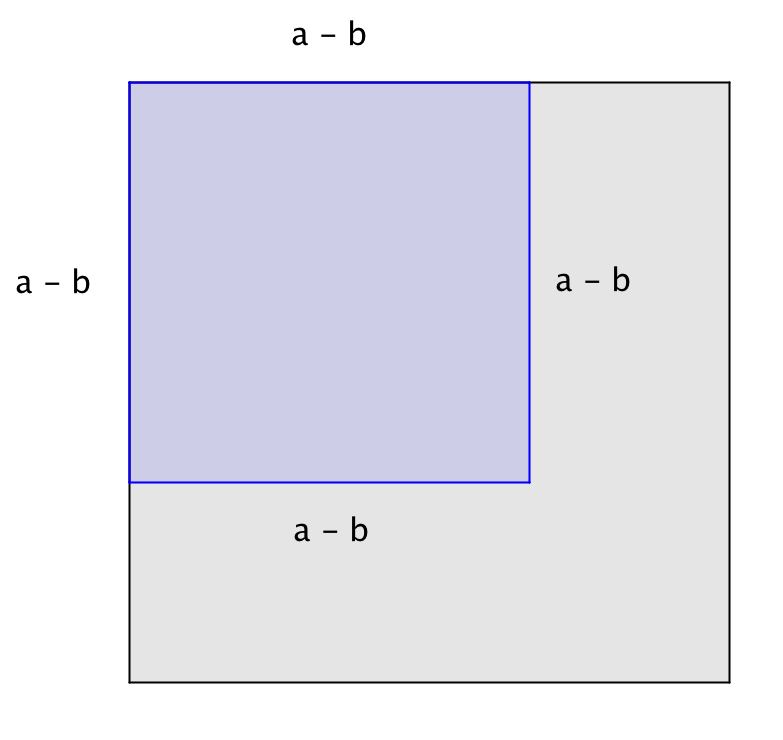
2) двух прямоугольников со сторонами \(\displaystyle a,\) и \(\displaystyle b,\)

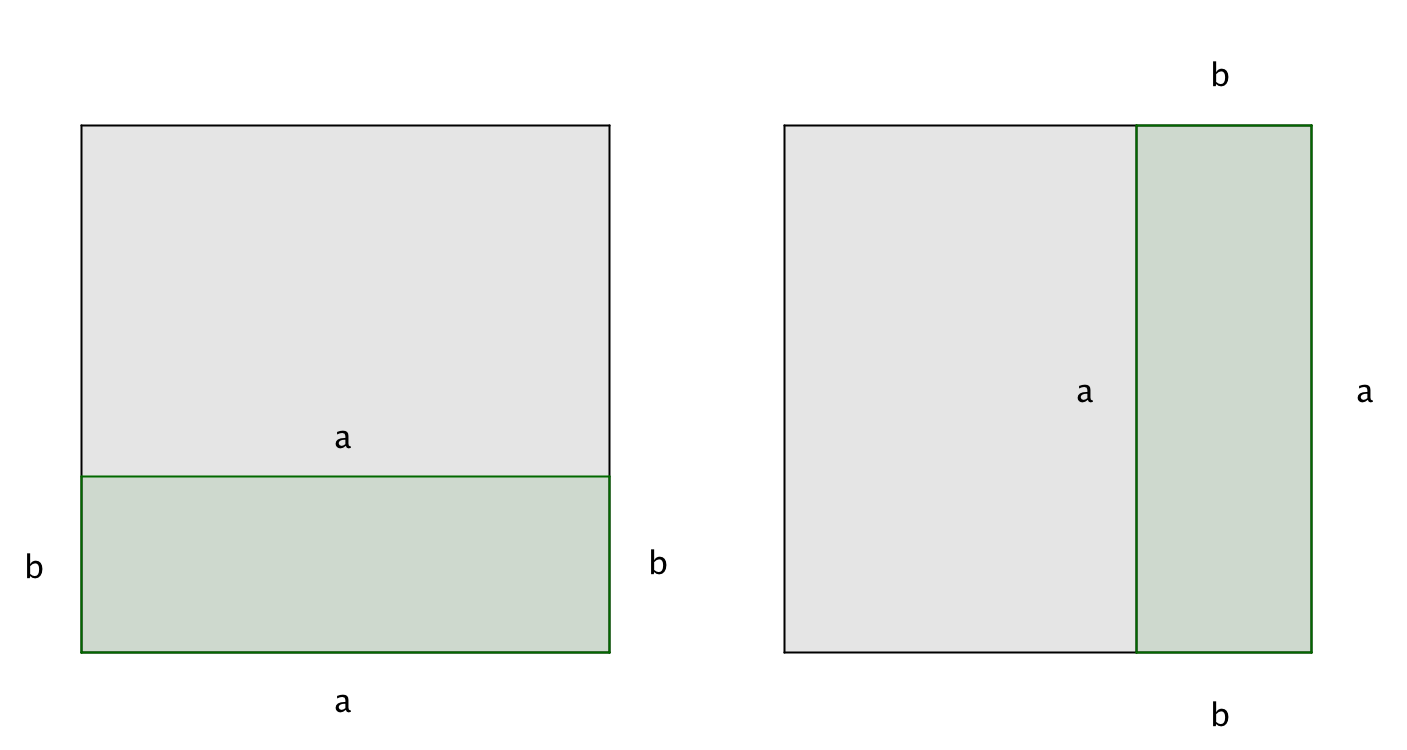
за исключением квадрата со стороной \(\displaystyle b:\)

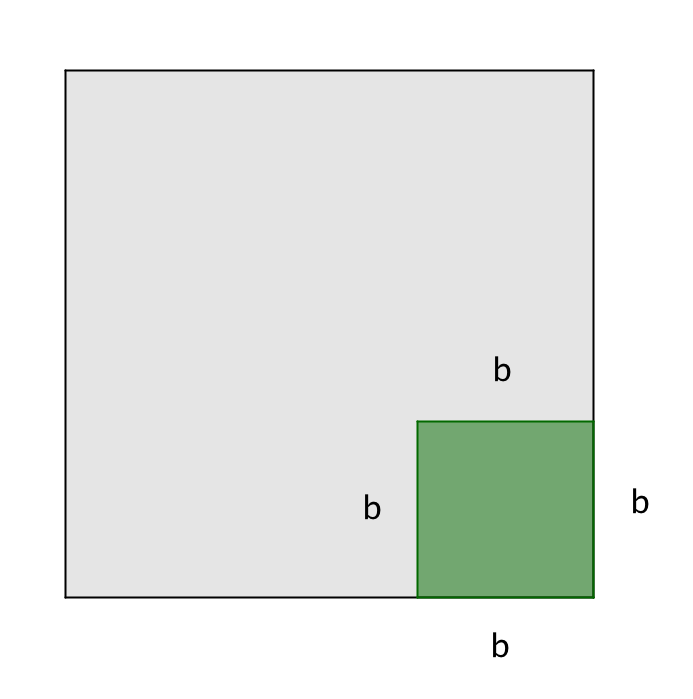
Поэтому площадь квадрата со стороной \(\displaystyle a\) равна сумме площадей квадрата со стороной \(\displaystyle a-b\), двух прямоугольников со сторонами \(\displaystyle a\) и \(\displaystyle b\) за вычетом площади квадрата со стороной \(\displaystyle b.\)

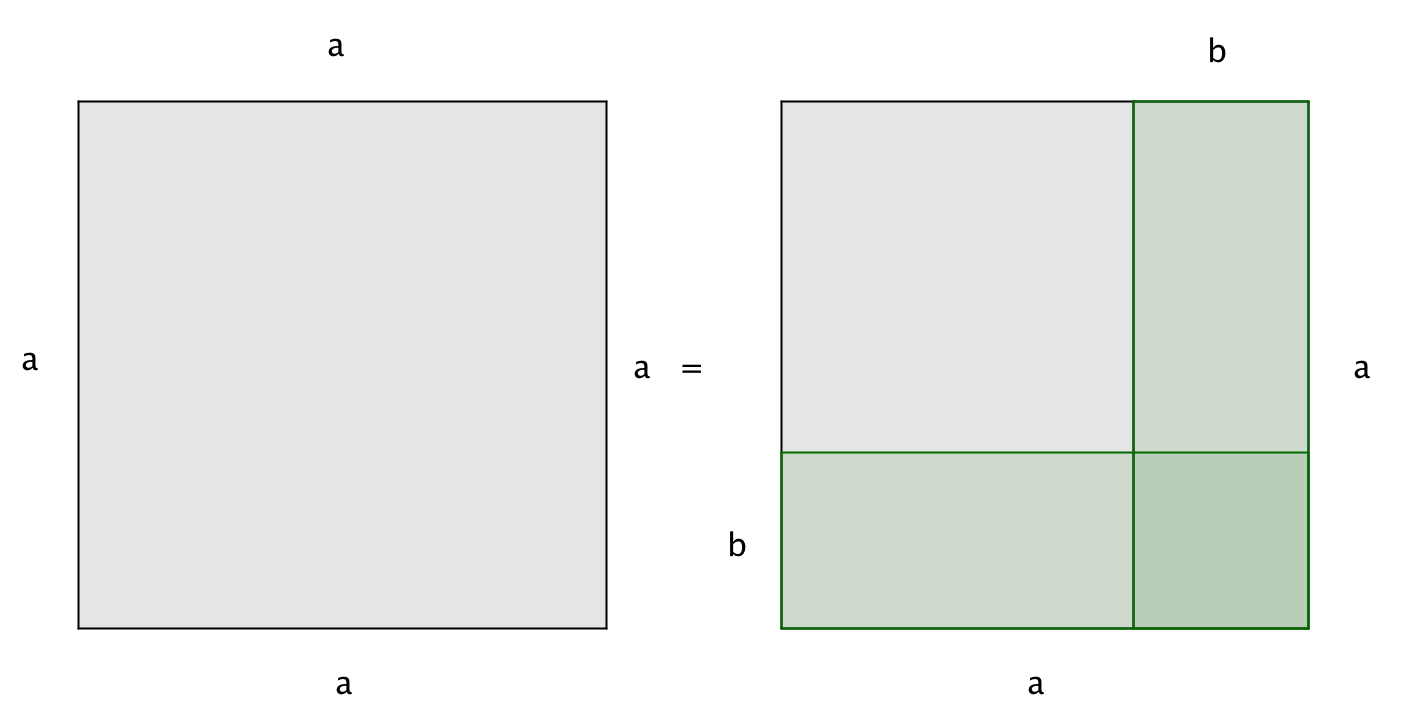
Площадь большого квадрата равна сумме площадей фигур из которых он составлен:

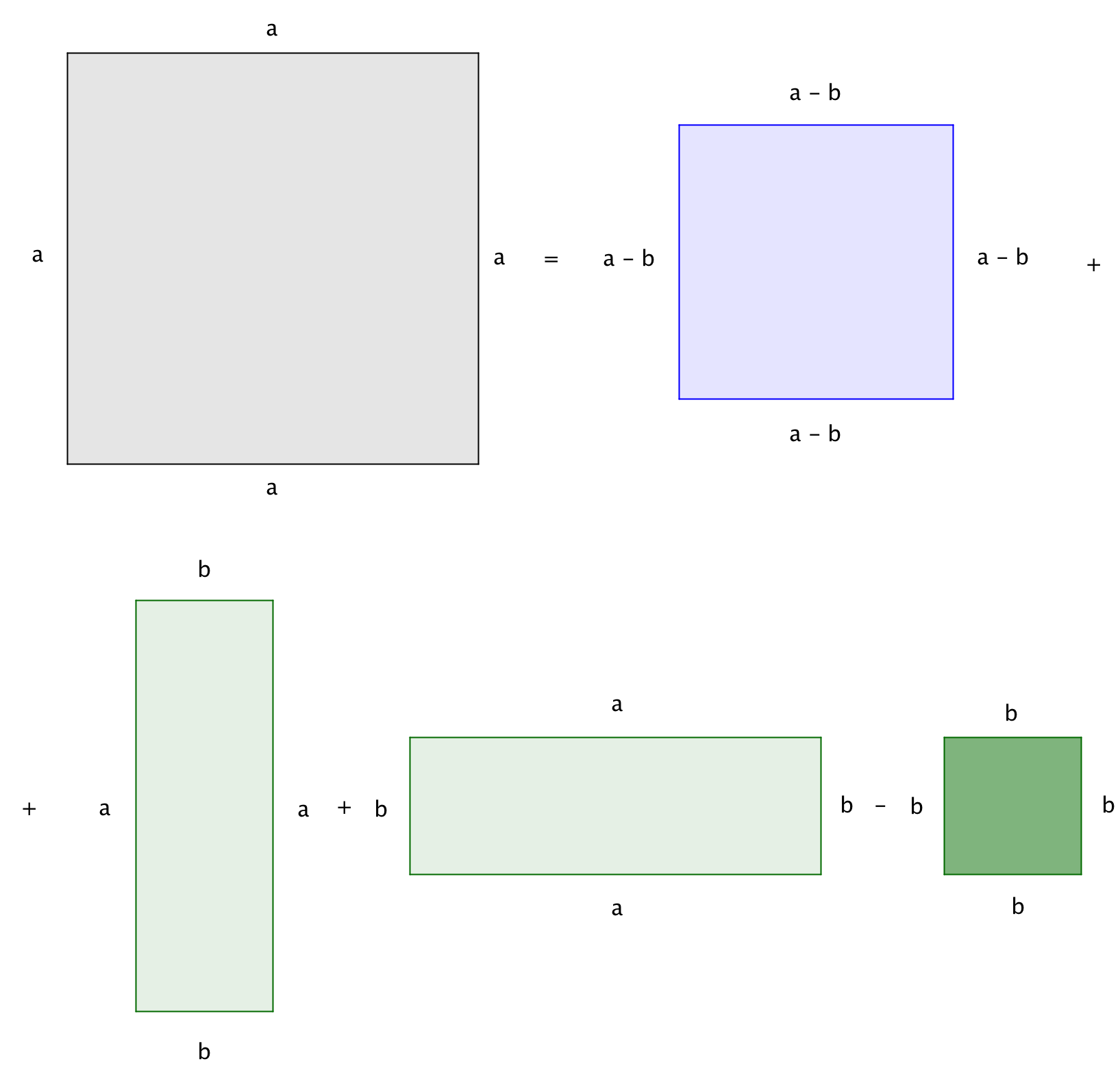
Найдем площадь каждой из фигур.

Площадь квадрата со стороной \(\displaystyle a\) равна \(\displaystyle a^{\,2}\):

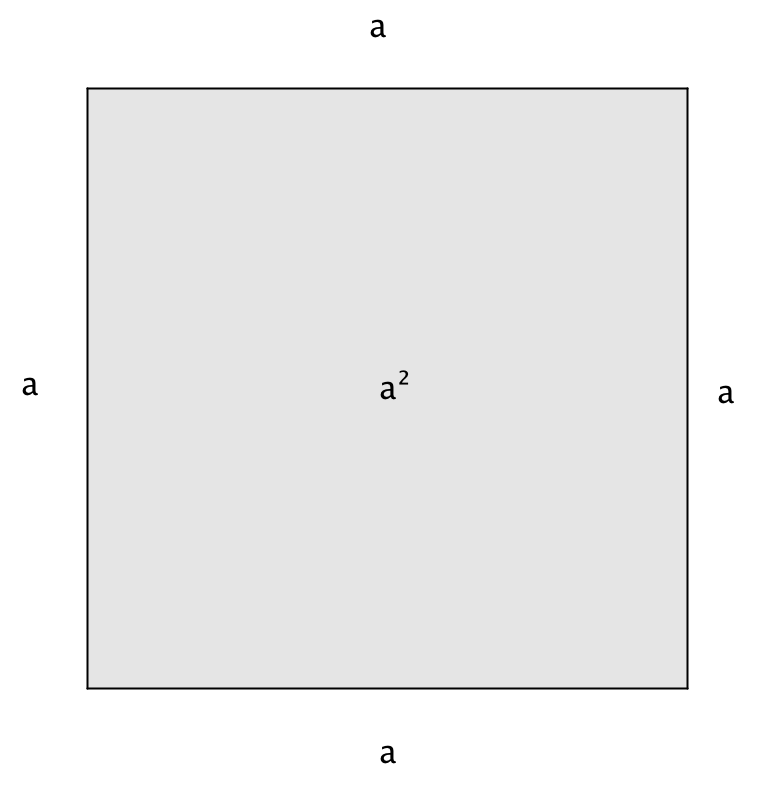\(\displaystyle =a^{\,2}\)

Площадь квадрата со стороной \(\displaystyle a - b\) равна \(\displaystyle (a-b\,)^2\):

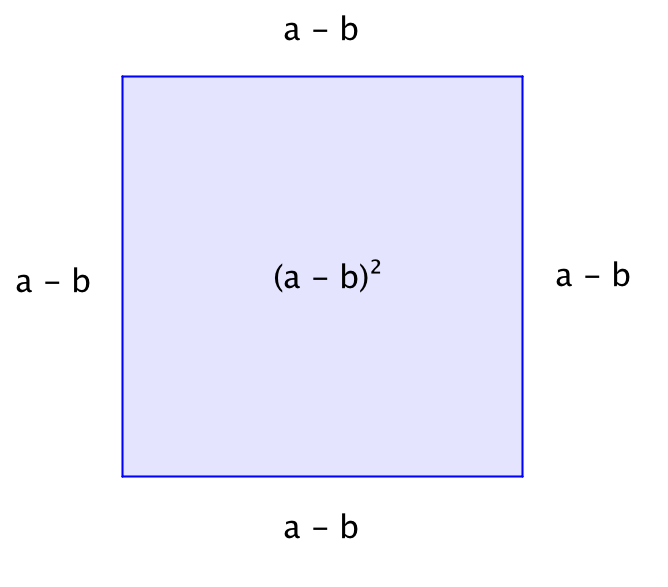\(\displaystyle =(a-b\,)^2\)

Площадь каждого из прямоугольков со сторонами \(\displaystyle a\) и \(\displaystyle b\) равна \(\displaystyle ab\):

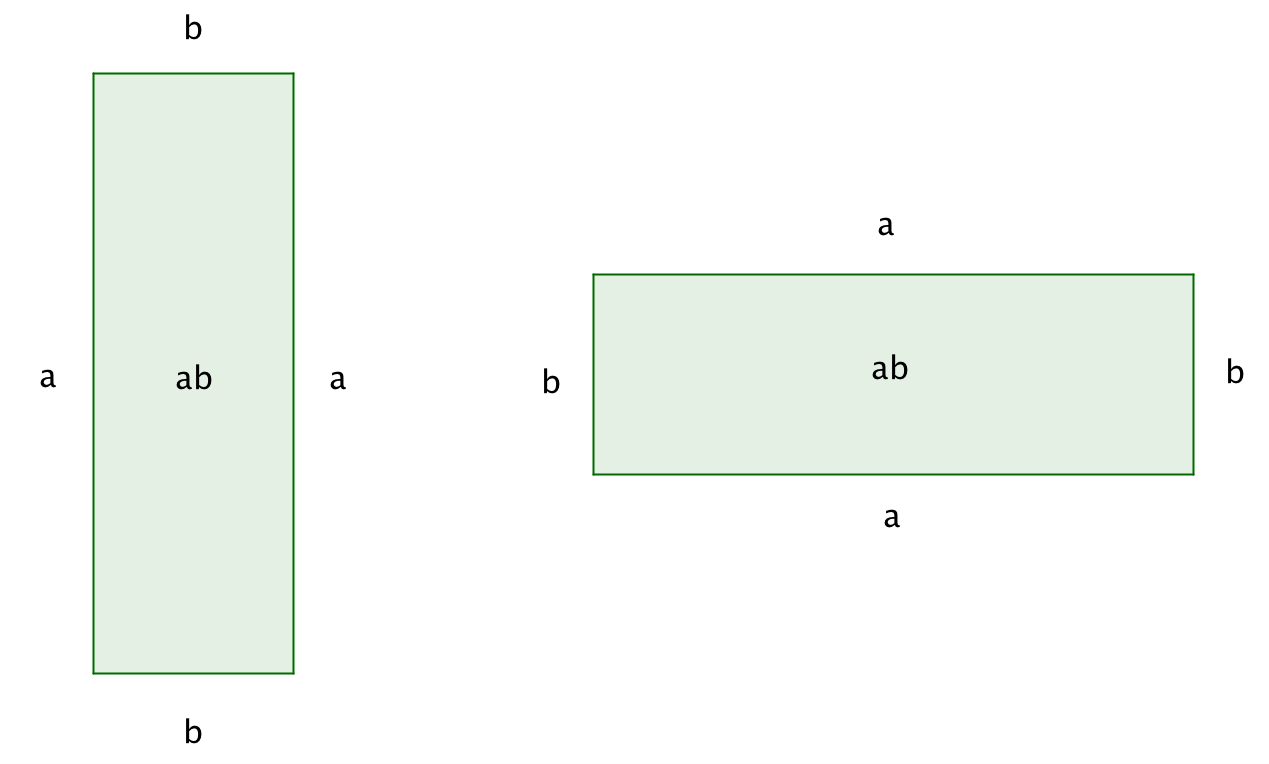\(\displaystyle =ab\)

Площадь квадрата со стороной \(\displaystyle b\) равна \(\displaystyle b^{\,2}\):

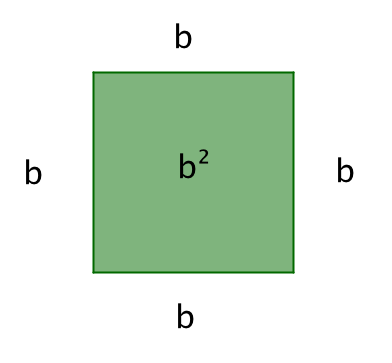\(\displaystyle =b^{\,2}\)

Найдем площадь квадрата со стороной \(\displaystyle a\) двумя способами: по определению и как сумму площадей фигур, из которых он составлен.

\(\displaystyle a^{\,2}=\)

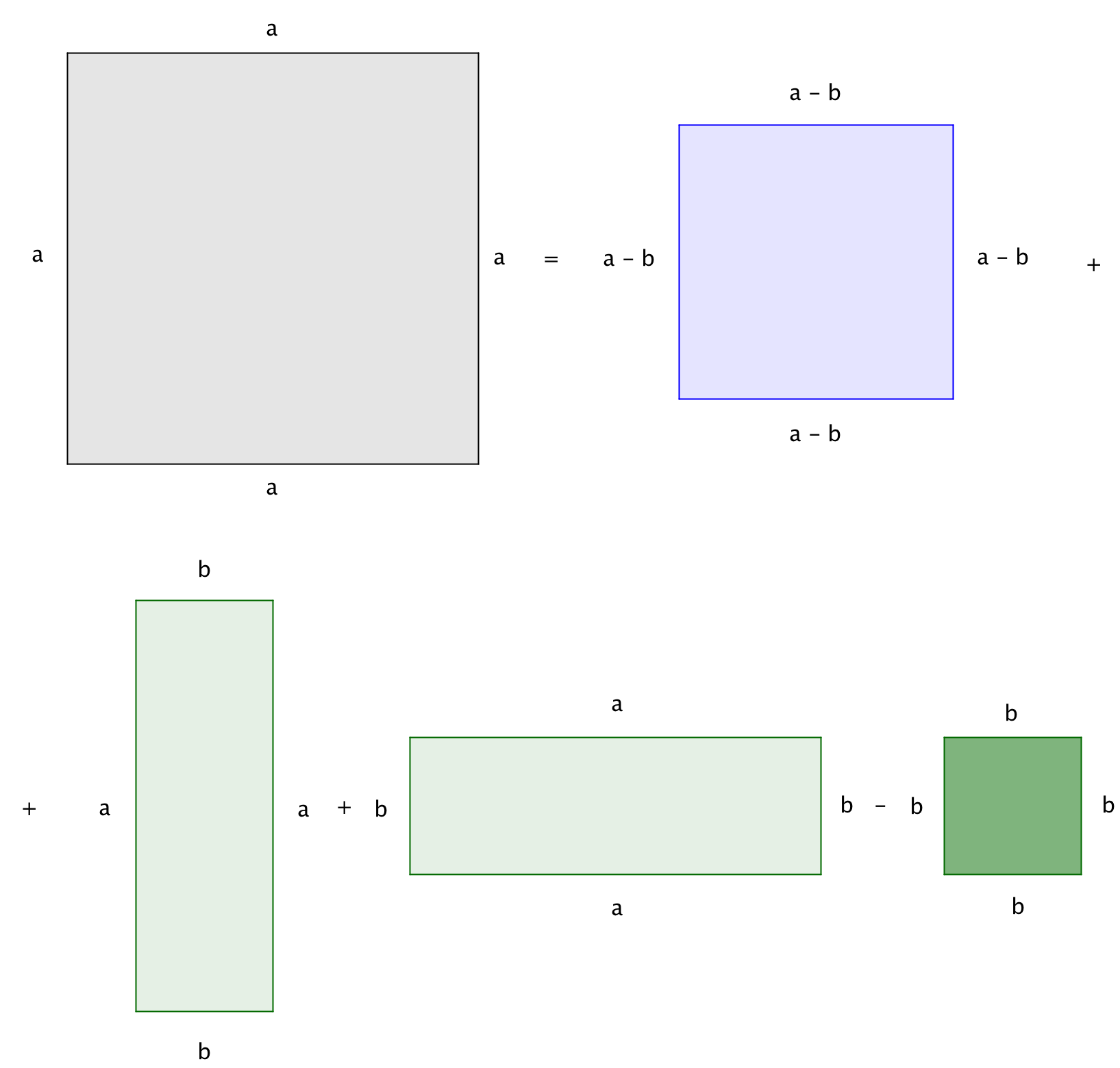\(\displaystyle =(a-b\,)^2+\underbrace{a\cdot b+a\cdot b}_{2ab}-b^{\,2}=(a-b\,)^2+2ab-b^{\,2}\)

Таким образом мы получили формулу,

\(\displaystyle a^{\,2}=(a-b\,)^2+2ab-b^{\,2},\)

откуда

\(\displaystyle (a-b\,)^2=a^{\,2}-2ab+b^{\,2}.\)