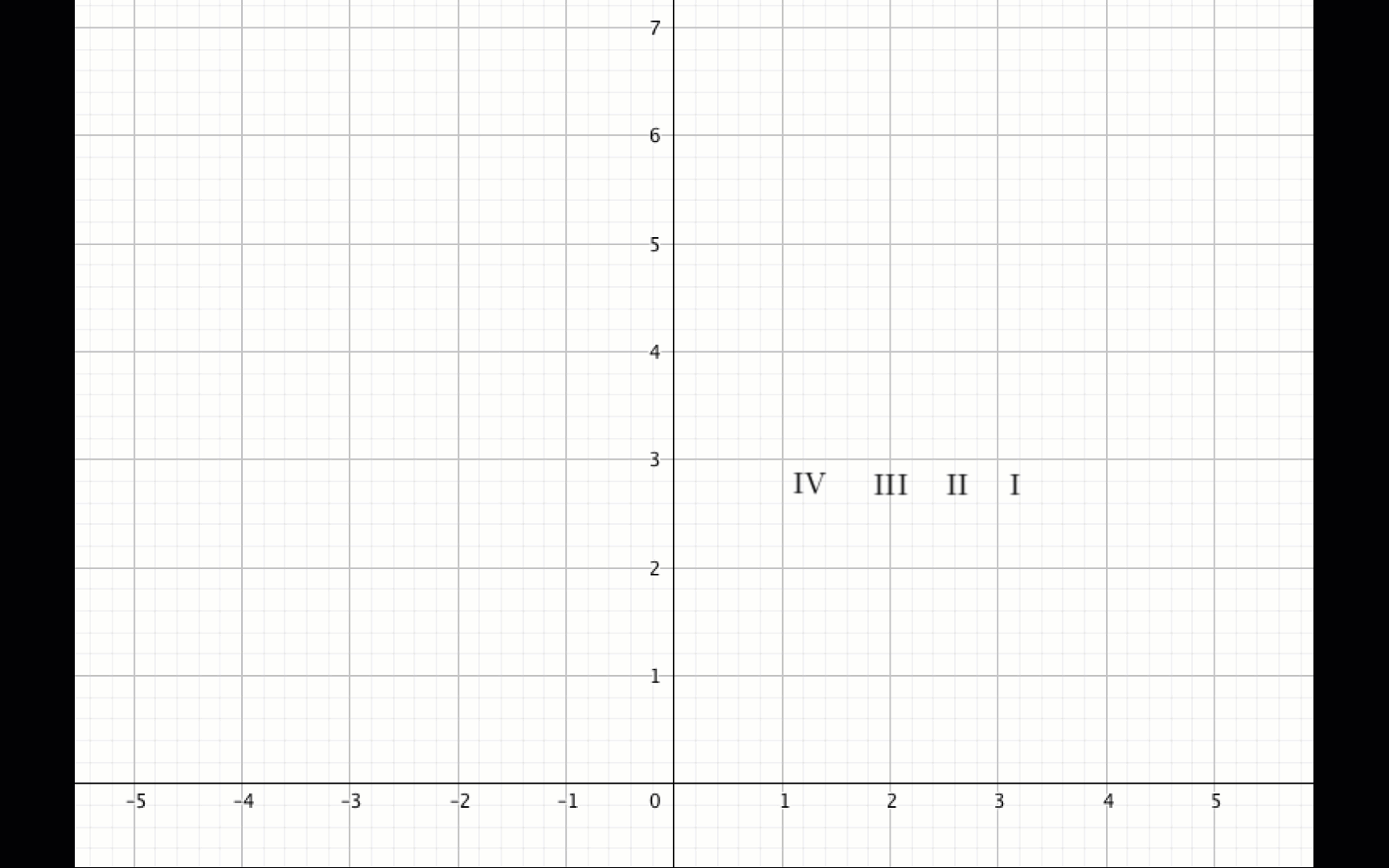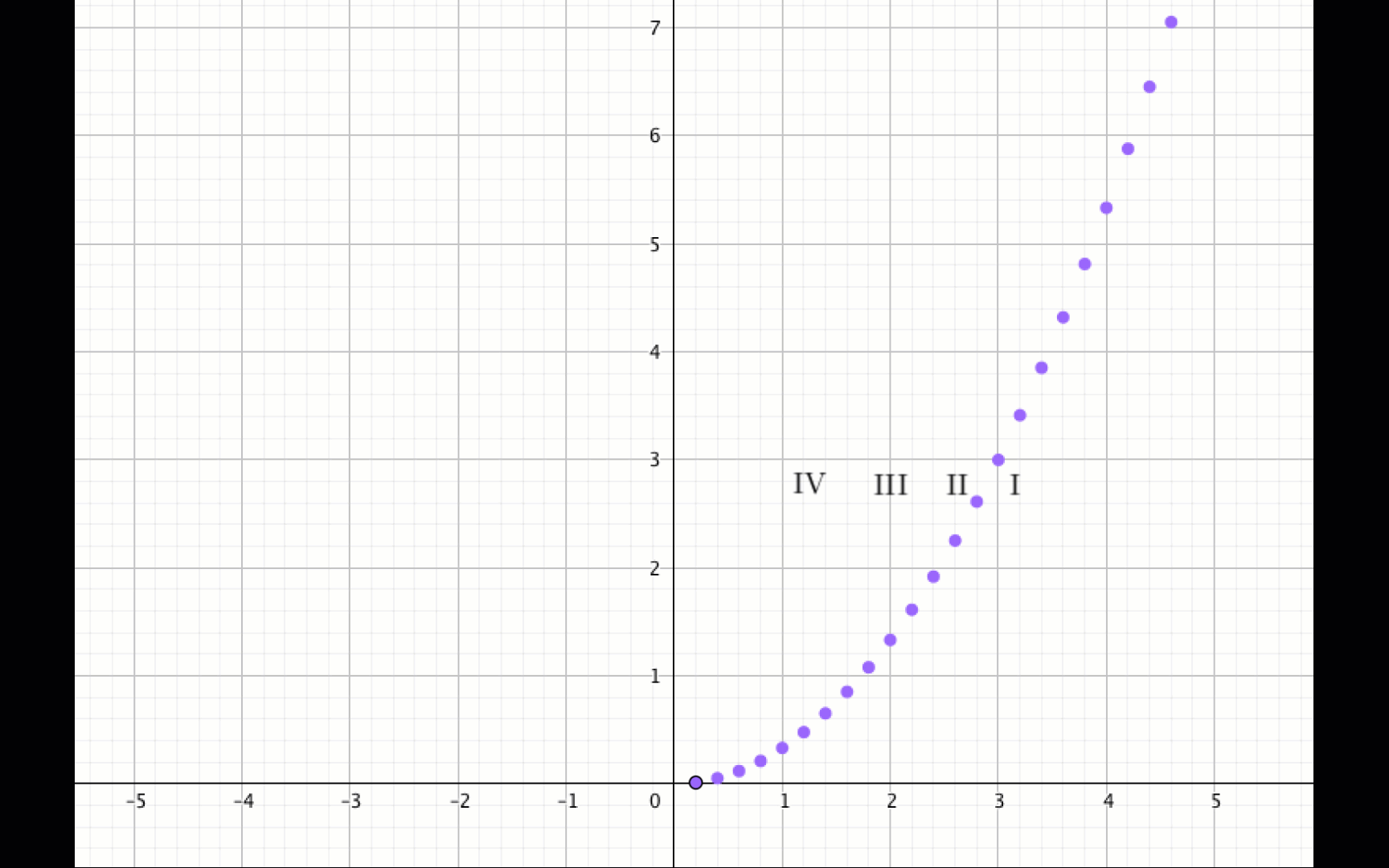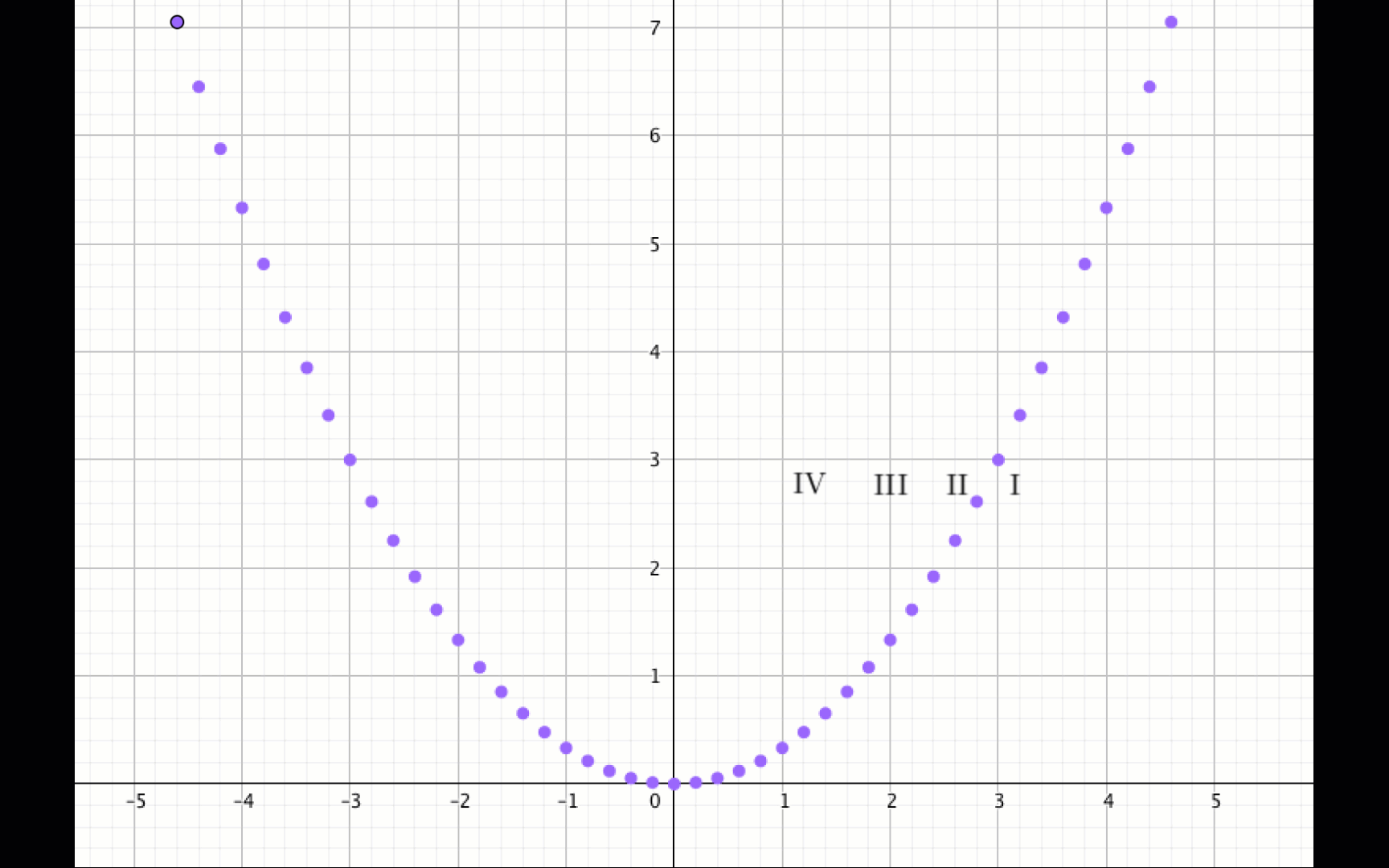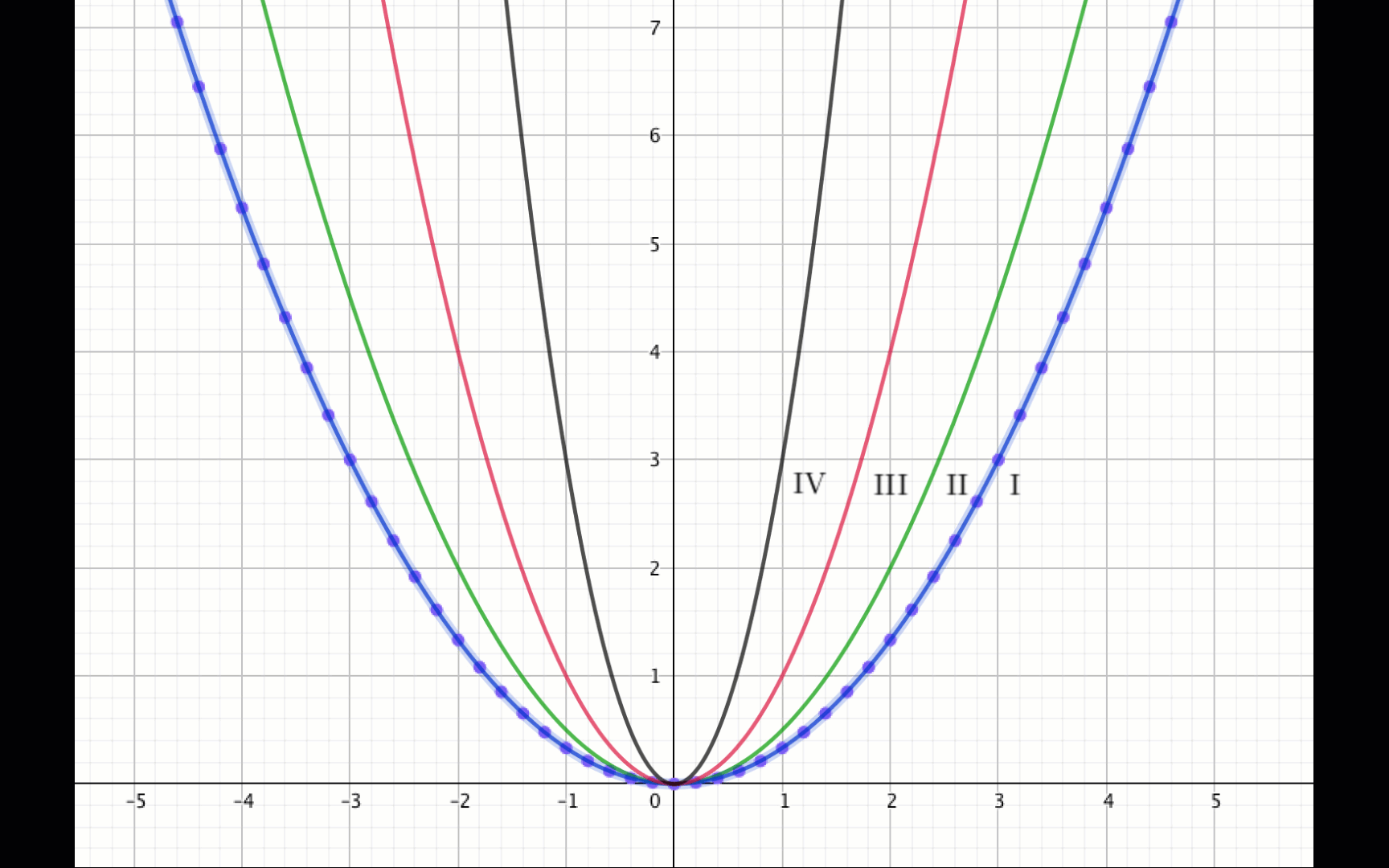Выберите параболу, соответствующую графику квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small : }\)
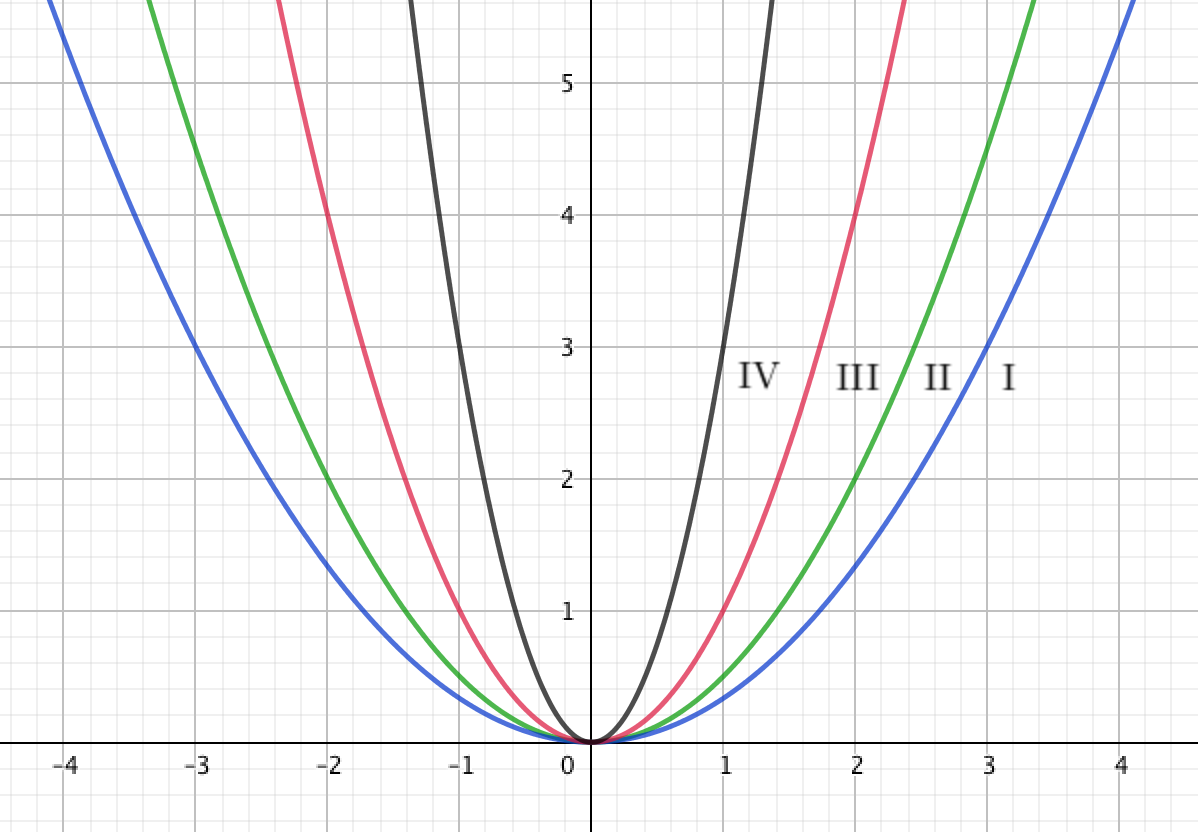
1. График \(\displaystyle \rm I {\small.}\)
На графике видно, что парабола \(\displaystyle \rm I\) проходит через точку с координатами \(\displaystyle (3;\, 3){\small : }\)
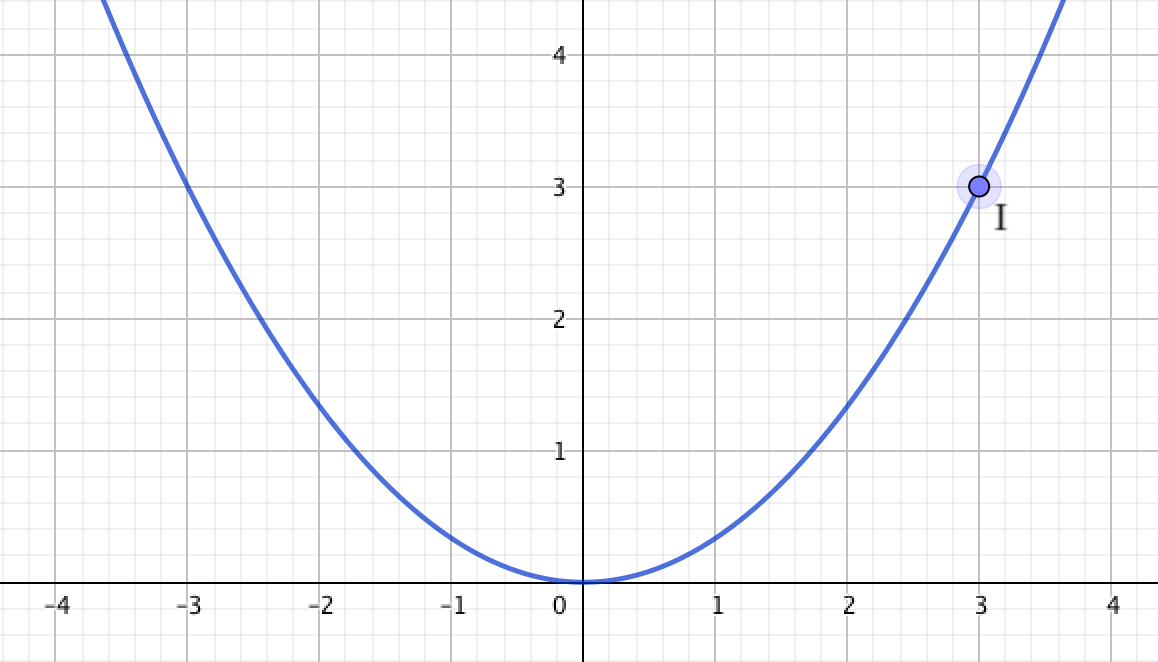
Проверим, лежит ли данная точка на графике квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small ,}\) подставляя её координаты в уравнение:
\(\displaystyle 3=\frac{1}{3}\cdot 3^2{\small ,}\)
\(\displaystyle 3=\frac{1}{3}\cdot 9{\small ,}\)
\(\displaystyle 3=3{\small .}\)
Получили верное равенство.
Значит, данная точка лежит на графике квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small .}\)
2. График \(\displaystyle \rm II {\small.}\)
На графике видно, что парабола \(\displaystyle \rm II\) проходит через точку с координатами \(\displaystyle (2;\, 2){\small : }\)
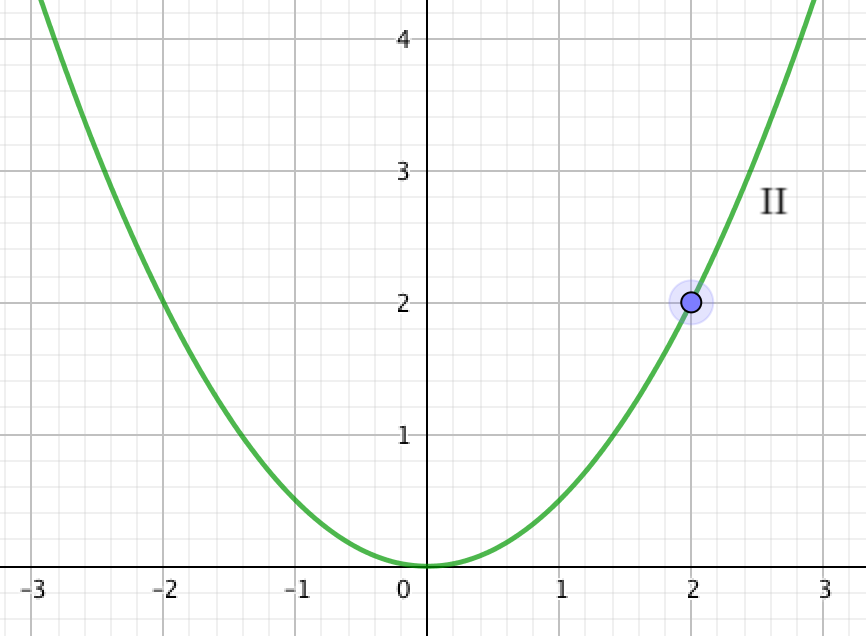
Проверим, лежит ли данная точка на графике квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small ,}\) подставляя её координаты в уравнение:
\(\displaystyle 2=\frac{1}{3}\cdot 2^2{\small ,}\)
\(\displaystyle 2=\frac{1}{3}\cdot 4{\small ,}\)
\(\displaystyle 2 =\frac{4}{3}{\small .}\)
Получили неверное равенство.
Значит, данная точка не лежит на графике квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small .}\)
Таким образом, парабола \(\displaystyle \rm II\) не является графиком квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small .}\)
3. График \(\displaystyle \rm III {\small.}\)
На графике видно, что парабола \(\displaystyle \rm III\) проходит через точку с координатами \(\displaystyle (2;4){\small : }\)
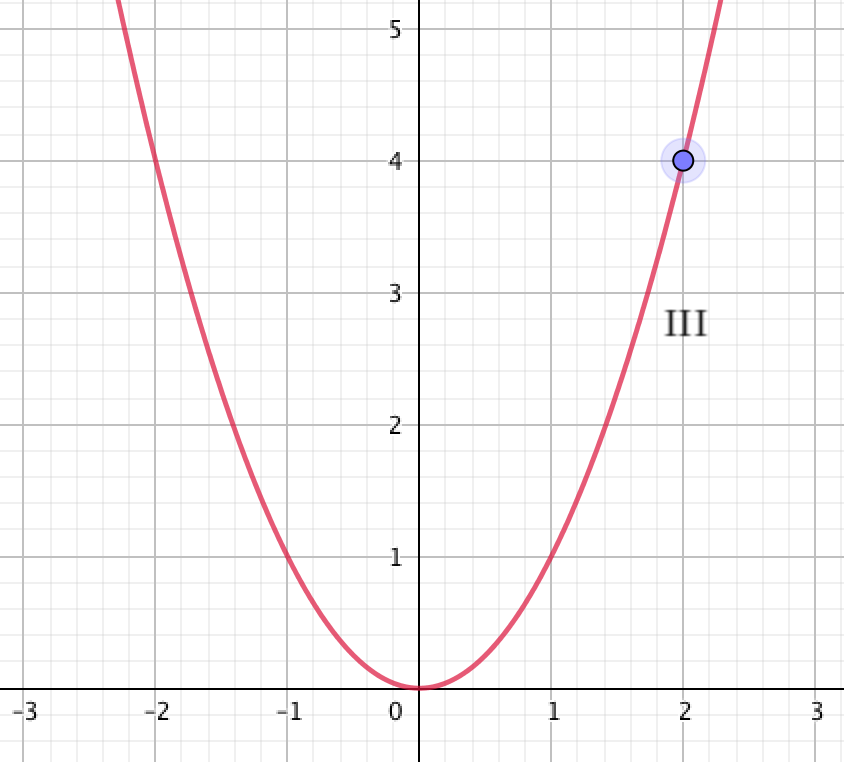
Проверим, лежит ли данная точка на графике квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small ,}\) подставляя её координаты в уравнение:
\(\displaystyle 4=\frac{1}{3}\cdot 2^2{\small ,}\)
\(\displaystyle 4=\frac{1}{3}\cdot 4{\small ,}\)
\(\displaystyle 4 =\frac{4}{3}{\small .}\)
Получили неверное равенство.
Значит, данная точка не лежит на графике квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small .}\)
Таким образом, парабола \(\displaystyle \rm III\) не является графиком квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small .}\)
4. График \(\displaystyle \rm IV {\small.}\)
На графике видно, что парабола \(\displaystyle \rm IV\) проходит через точку с координатами \(\displaystyle (1;\, 3){\small : }\)
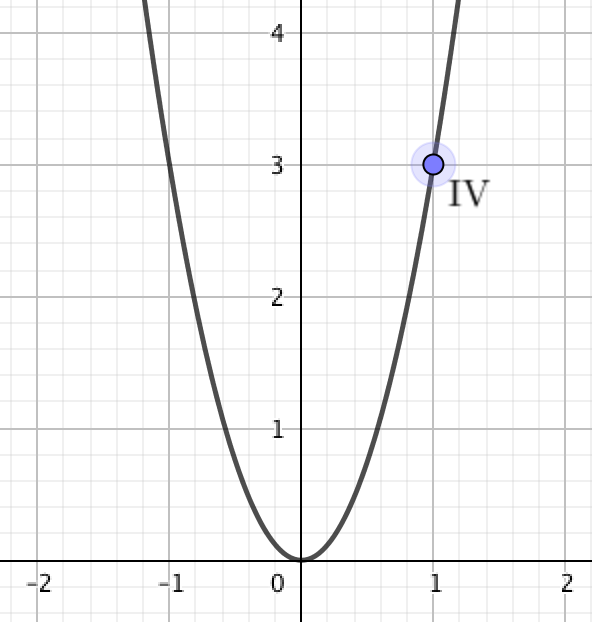
Проверим, лежит ли данная точка на графике квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small ,}\) подставляя её координаты в уравнение:
\(\displaystyle 3=\frac{1}{3}\cdot 1^2{\small ,}\)
\(\displaystyle 3=\frac{1}{3}\cdot 1{\small ,}\)
\(\displaystyle 3 =\frac{1}{3}{\small .}\)
Получили неверное равенство.
Значит, данная точка не лежит на графике квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small .}\)
Таким образом, парабола \(\displaystyle \rm IV\) не является графиком квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small .}\)
Следовательно, парабола \(\displaystyle \rm I\) является графиком квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small .}\)
Ответ: \(\displaystyle \rm I {\small .}\)
Построим график квадратичной функции \(\displaystyle y=\frac{1}{3}x^2{\small, }\) вычисляя значения функции в точках: