Дана квадратичная функция \(\displaystyle y=x^2{\small .}\) Вычислите значения функции в заданных точках:
| \(\displaystyle x\) | \(\displaystyle -2\) | \(\displaystyle -1{,}7\) | \(\displaystyle -1{,}5\) | \(\displaystyle -1\) | \(\displaystyle -0{,}5\) | \(\displaystyle 0\) | \(\displaystyle 0{,}5\) | \(\displaystyle 1\) | \(\displaystyle 1{,}5\) | \(\displaystyle 1{,}7\) | \(\displaystyle 2\) |
| \(\displaystyle y=x^2\) |
Выберите правильный график с точками, лежащими на этой квадратичной функции \(\displaystyle y=x^2{\small :}\)
| \(\displaystyle \rm I\) | \(\displaystyle \rm II\) |
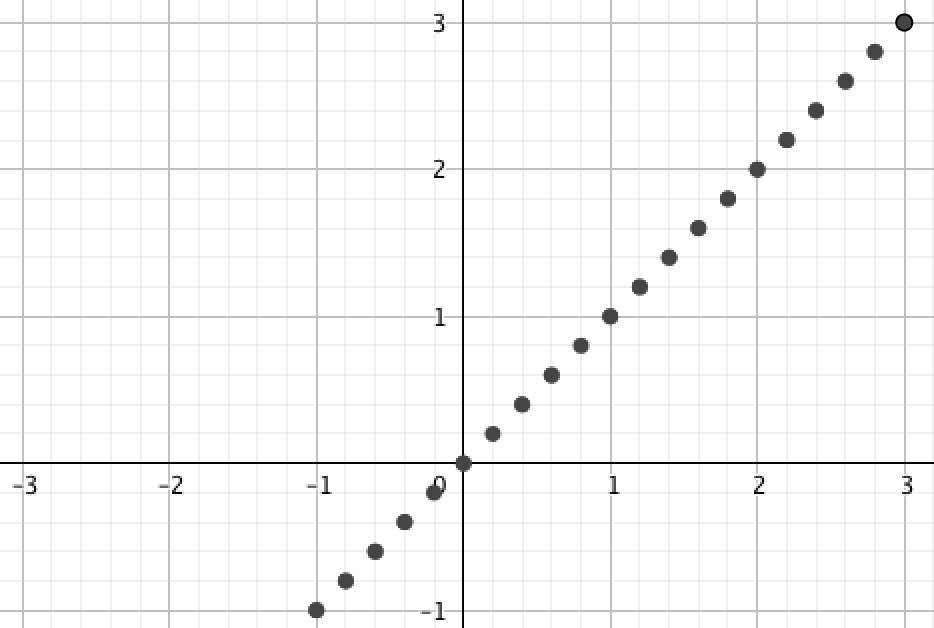 | 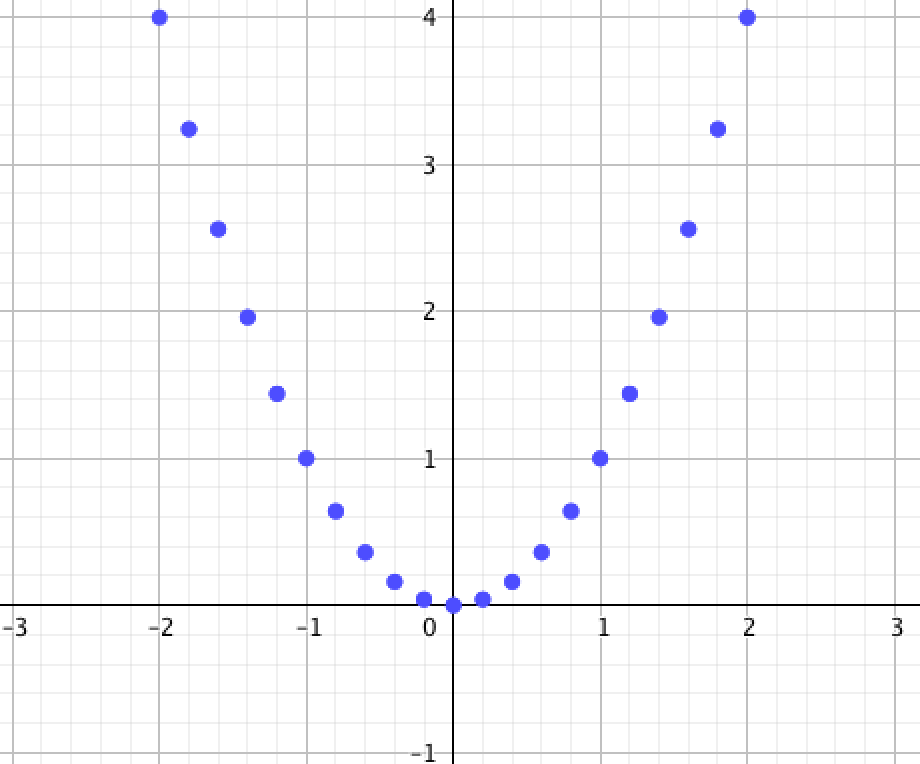 |
| \(\displaystyle \rm III\) | \(\displaystyle \rm IV\) |
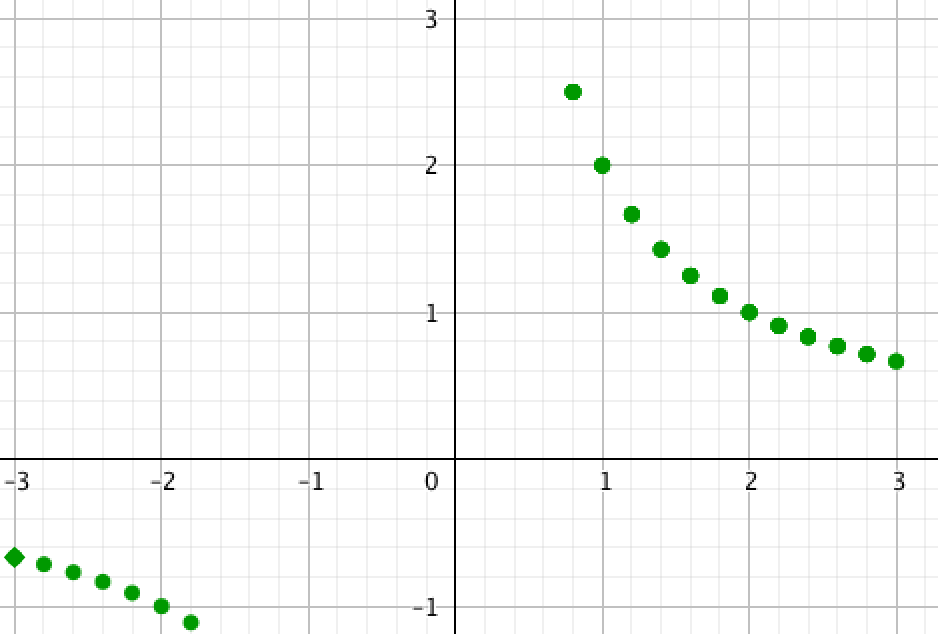 | 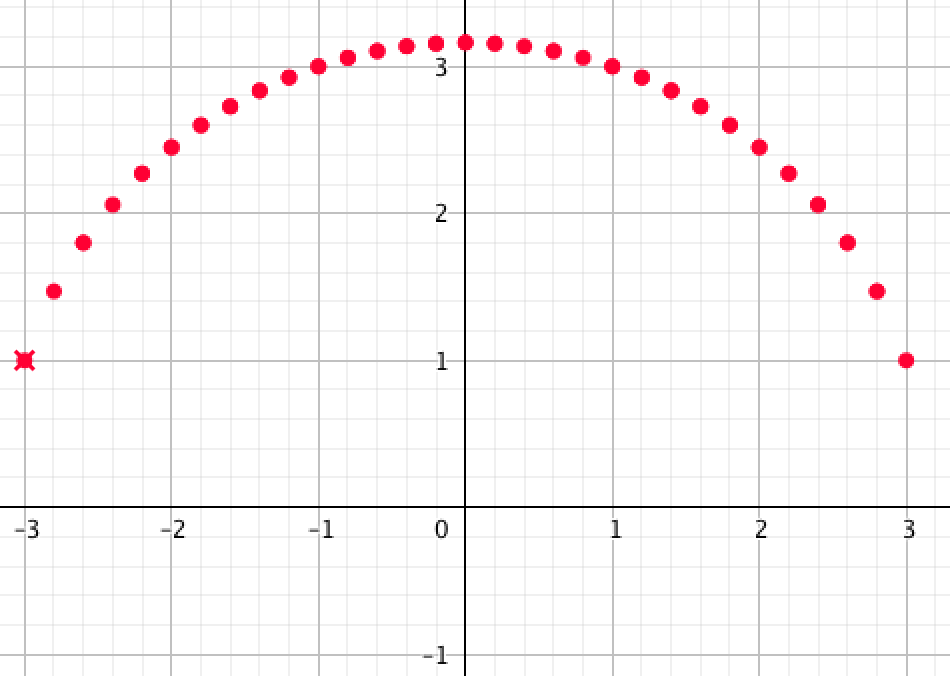 |
Вычислим значение квадратичной функции \(\displaystyle y=x^2\) в заданных точках:
| \(\displaystyle x\) | \(\displaystyle -2\) | \(\displaystyle -1{,}7\) | \(\displaystyle -1{,}5\) | \(\displaystyle -1\) | \(\displaystyle -0{,}5\) | \(\displaystyle 0\) | \(\displaystyle 0{,}5\) | \(\displaystyle 1\) | \(\displaystyle 1{,}5\) | \(\displaystyle 1{,}7\) | \(\displaystyle 2\) |
| \(\displaystyle y=x^2\) | \(\displaystyle 4\) | \(\displaystyle 2{,}89\) | \(\displaystyle 2{,}25\) | \(\displaystyle 1\) | \(\displaystyle 0{,}25\) | \(\displaystyle 0\) | \(\displaystyle 0{,}25\) | \(\displaystyle 1\) | \(\displaystyle 2{,}25\) | \(\displaystyle 2{,}89\) | \(\displaystyle 4\) |
Отметим точки
\(\displaystyle (-2;\, 4),\, (-1{,}7;\, 2{,}89),\, (-1{,}5;\, 2{,}25),\, (-1;\, 1),\, (-0{,}5;\, 0{,}25),\, (0;\, 0),\)
\(\displaystyle (0{,}5;\, 0{,}25),\, (1;\, 1),\, (1{,}5;\, 2{,}25),\, (1{,}7;\, 2{,}89),\,(2;\, 4)\)
на координатной плоскости:
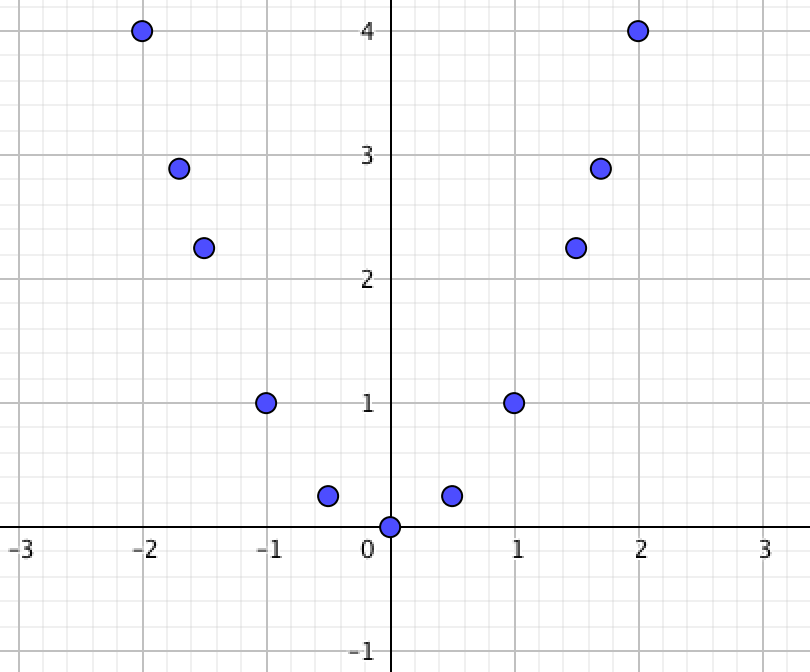
Сравним с данными графиками:
| \(\displaystyle \rm I\) | \(\displaystyle \rm II\) |
 |  |
| \(\displaystyle \rm III\) | \(\displaystyle \rm IV\) |
 |  |
Видим, что график \(\displaystyle \rm II\) соответствует нашей квадратичной функции \(\displaystyle y=x^2{\small .}\)
Ответ: \(\displaystyle \rm II {\small .}\)