Задание
Выберите верное соответствие:
| \(\displaystyle y=f^{\prime}(x)\) | \(\displaystyle y=f(x)\) |
 | |
 |
Решение
Правило
- Если в каждой точке \(\displaystyle x_0 \in (\alpha; \beta): f^{\prime}(x_0)>0{ \small ,}\) то функция \(\displaystyle f(x)\) возрастает на интервале \(\displaystyle (\alpha; \beta){\small .}\)
- Если в каждой точке \(\displaystyle x_0 \in (\alpha; \beta): f^{\prime}(x_0)<0{ \small ,}\) то функция \(\displaystyle f(x)\) убывает на интервале \(\displaystyle (\alpha; \beta){\small .}\)
--------Первый график---------
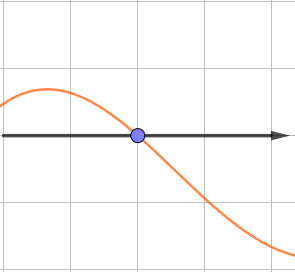
На первом графике производной функции \(\displaystyle y=f^{\prime}(x)\)

производная до точки пересечения положительна, после точки пересечения отрицательна.
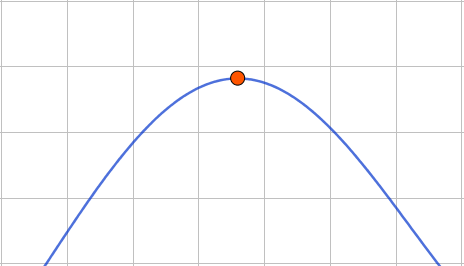
Поэтому на промежутке до точки пересечения функция возрастает, а после убывает:
| \(\displaystyle y=f^{\prime}(x)\) | \(\displaystyle +\) | точка пересечения | \(\displaystyle -\) |
| \(\displaystyle y=f(x)\) | \(\displaystyle \nearrow\) | максимум | \(\displaystyle \searrow\) |
--------Второй график---------
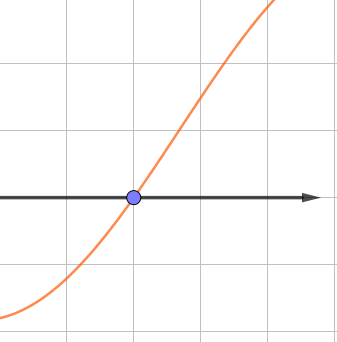
На втором графике производной функции \(\displaystyle y=f^{\prime}(x)\)

производная до точки пересечения отрицательна, после точки пересечения положительна.
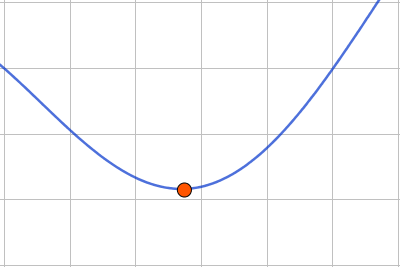
Поэтому на промежутке до точки пересечения функция убывает, а после возрастает:
| \(\displaystyle y=f^{\prime}(x)\) | \(\displaystyle -\) | точка пересечения | \(\displaystyle +\) |
| \(\displaystyle y=f(x)\) | \(\displaystyle \searrow\) | минимум | \(\displaystyle \nearrow\) |