Выберите точку, в абсциссе которой производная функции \(\displaystyle f^{\prime}(x)\) обращается в ноль.
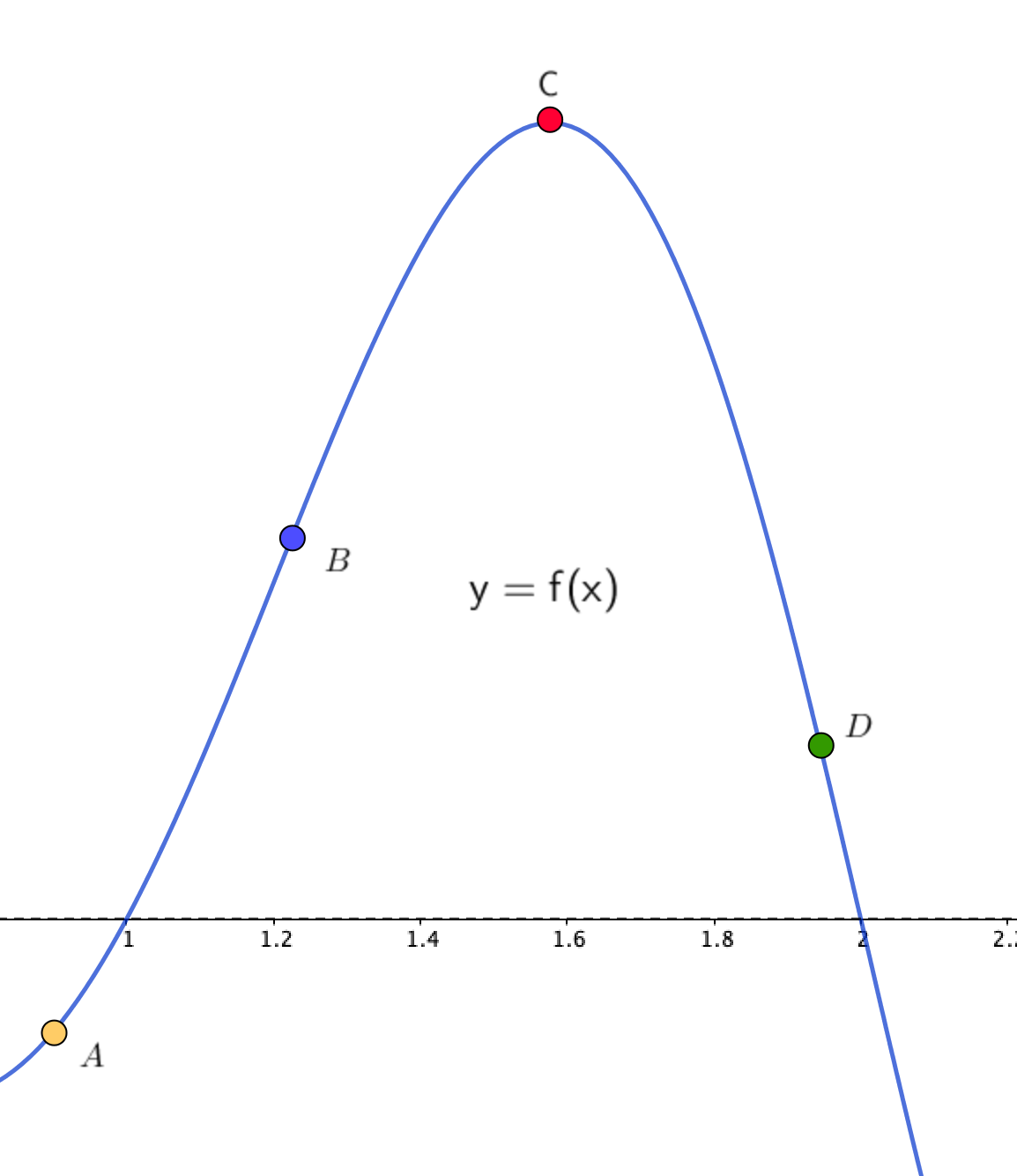
Значение производной в точке \(\displaystyle x_0\) равно \(\displaystyle \tg(\alpha){ \small ,}\) где \(\displaystyle \alpha \) – угол наклона касательной в соответствующей точке на кривой \(\displaystyle y=f(x){\small .}\)
Так как тангенс на промежутке \(\displaystyle [0;\pi) \) равен нулю только в нуле, то необходимо выбрать те точки, в которых касательная параллельна (или совпадает) оси \(\displaystyle \rm OX{\small .}\)
Построим касательные в каждой точке:
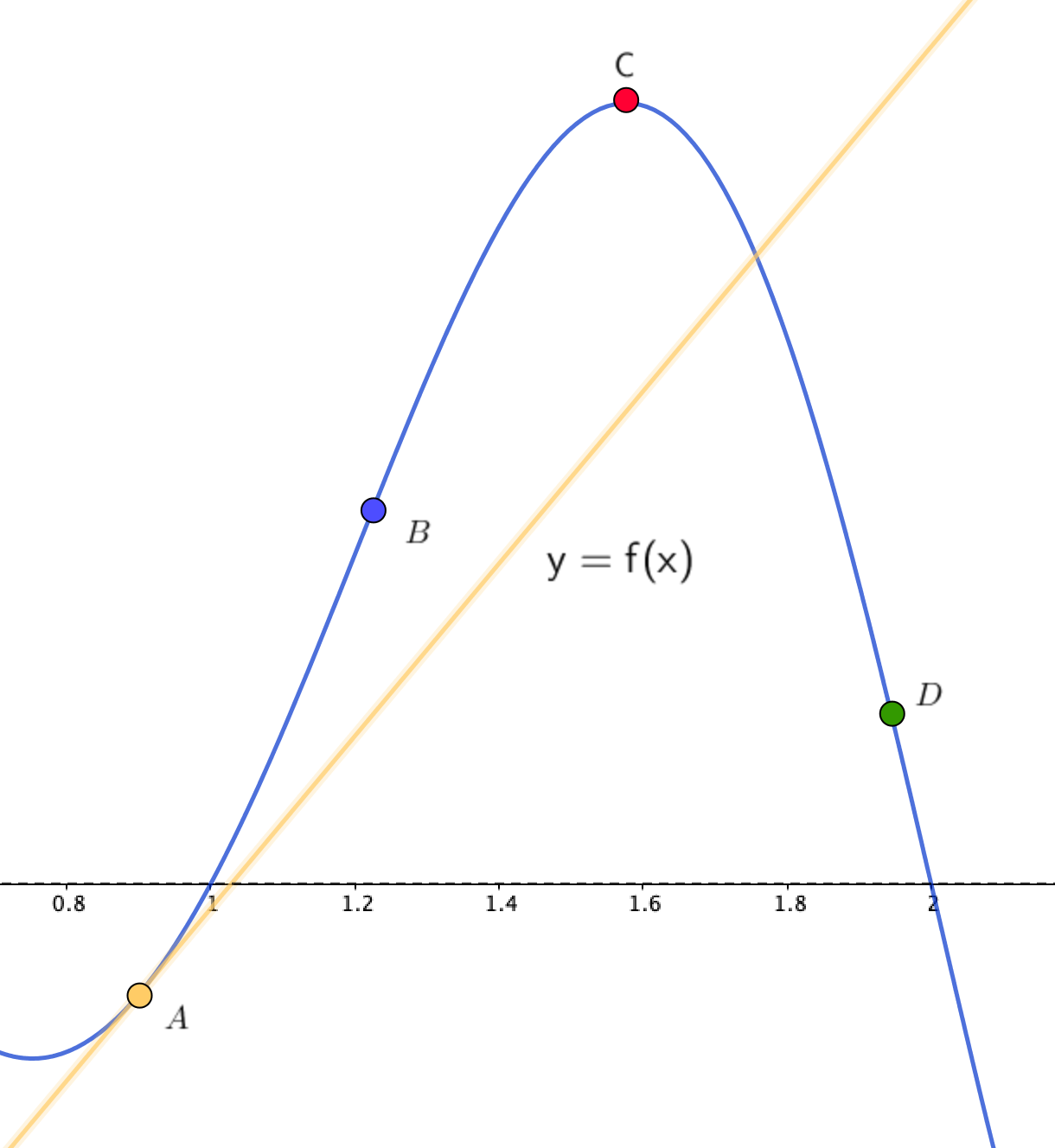
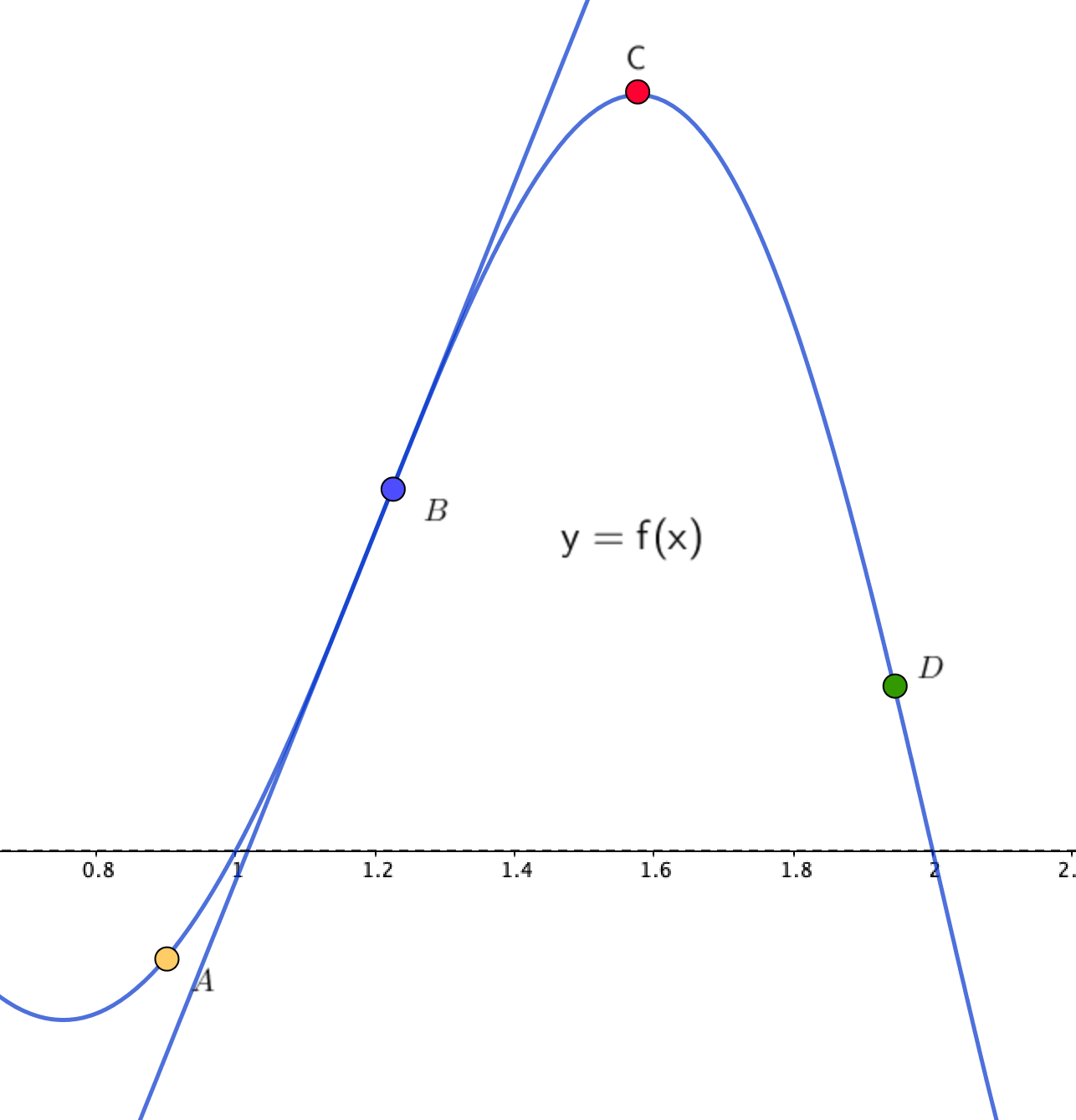
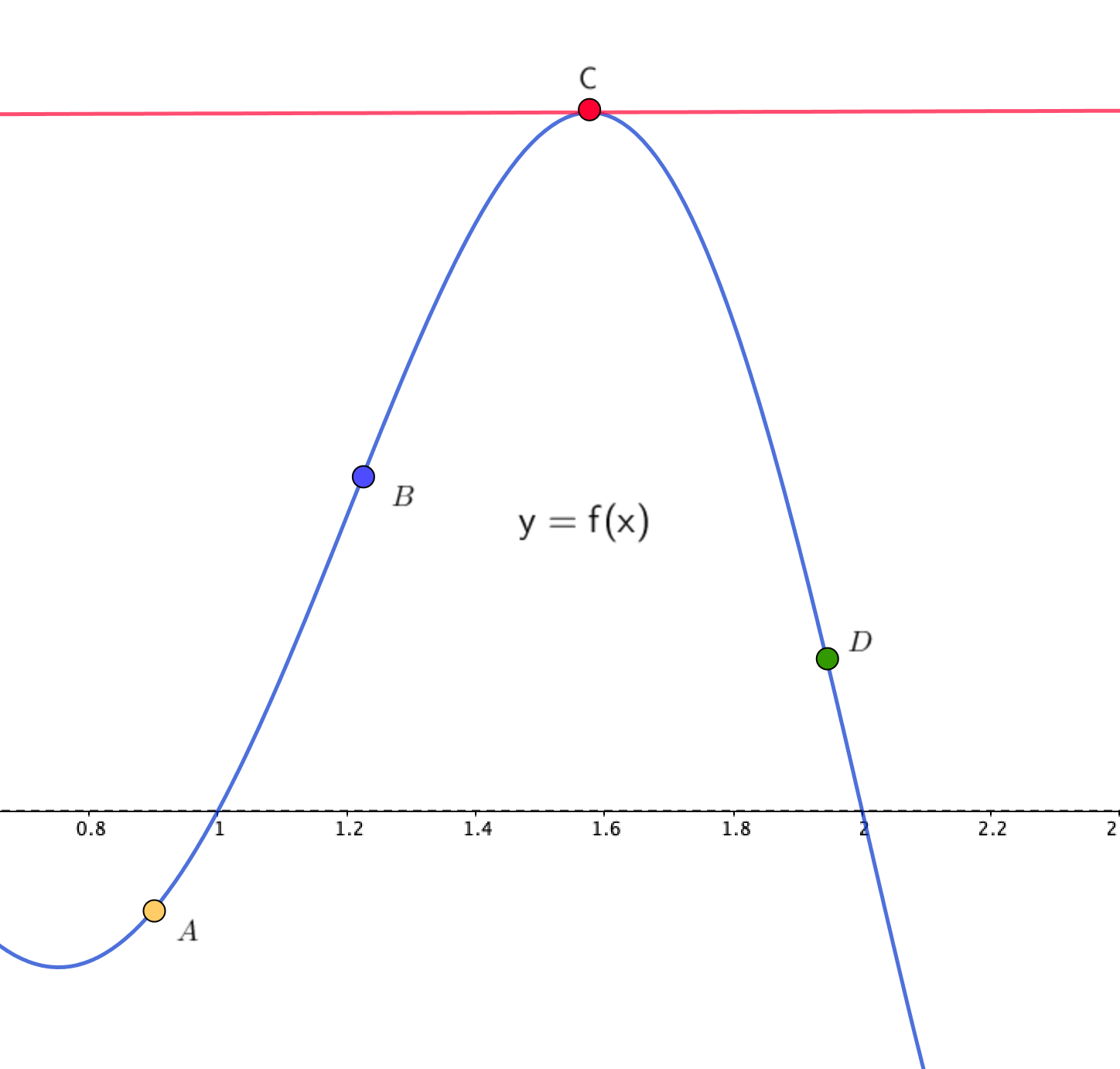
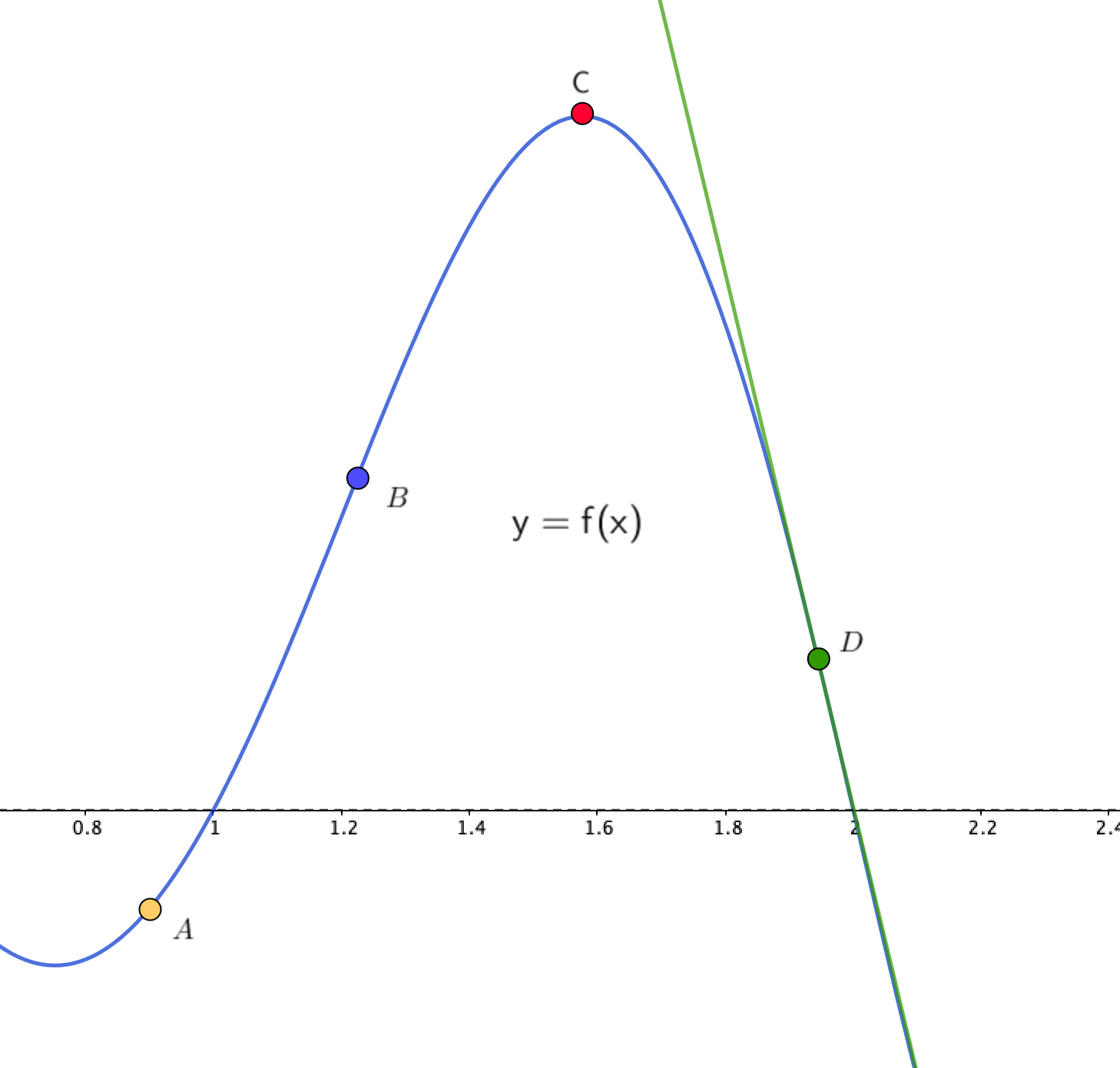
Так как в точке \(\displaystyle C\) касательная параллельна оси \(\displaystyle \rm OX{ \small ,}\) то в абсциссе этой точки производная обращается в ноль.
Ответ: \(\displaystyle C{\small .}\)