 | 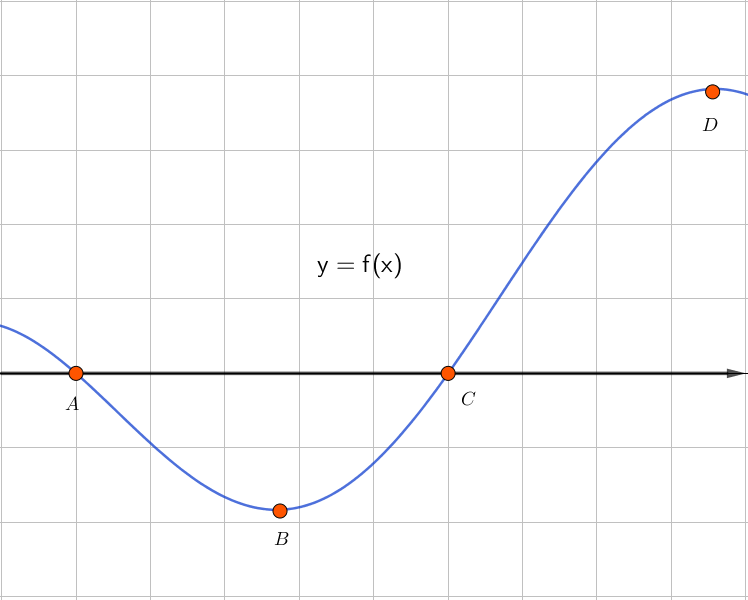 |
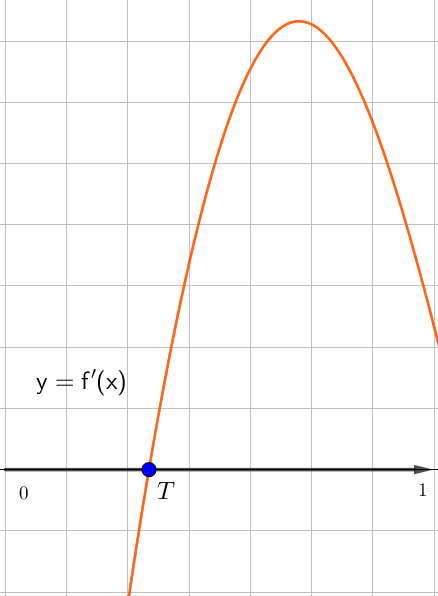
Какой точке на графике функции \(\displaystyle y=f(x)\) соответствует точка \(\displaystyle T\) графика производной функции \(\displaystyle y=f^{\prime}(x){\small ? }\)
- Если в каждой точке \(\displaystyle x_0 \in (\alpha; \beta): f^{\prime}(x_0)>0{ \small ,}\) то функция \(\displaystyle f(x)\) возрастает на интервале \(\displaystyle (\alpha; \beta){\small .}\)
- Если в каждой точке \(\displaystyle x_0 \in (\alpha; \beta): f^{\prime}(x_0)<0{ \small ,}\) то функция \(\displaystyle f(x)\) убывает на интервале \(\displaystyle (\alpha; \beta){\small .}\)
Промежуток, где производная отрицательна
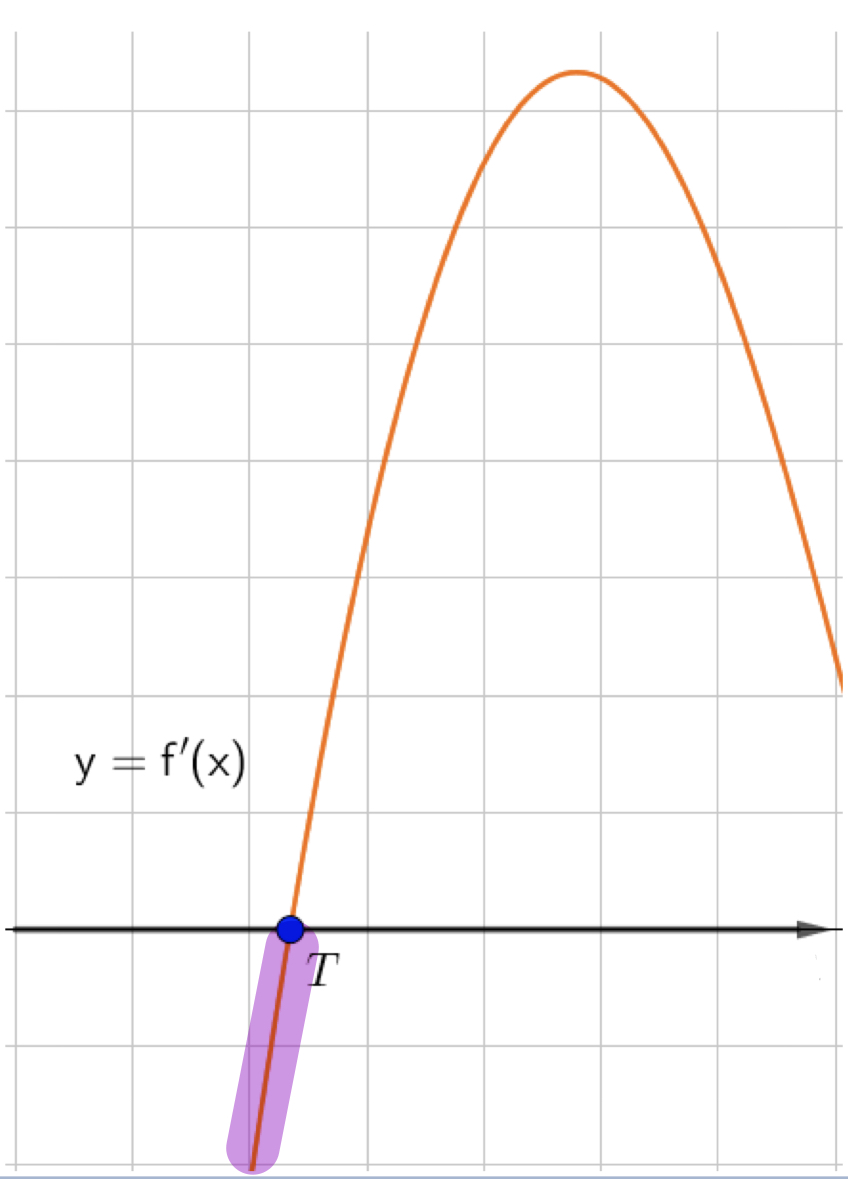
соответствует промежутку убывания функции:
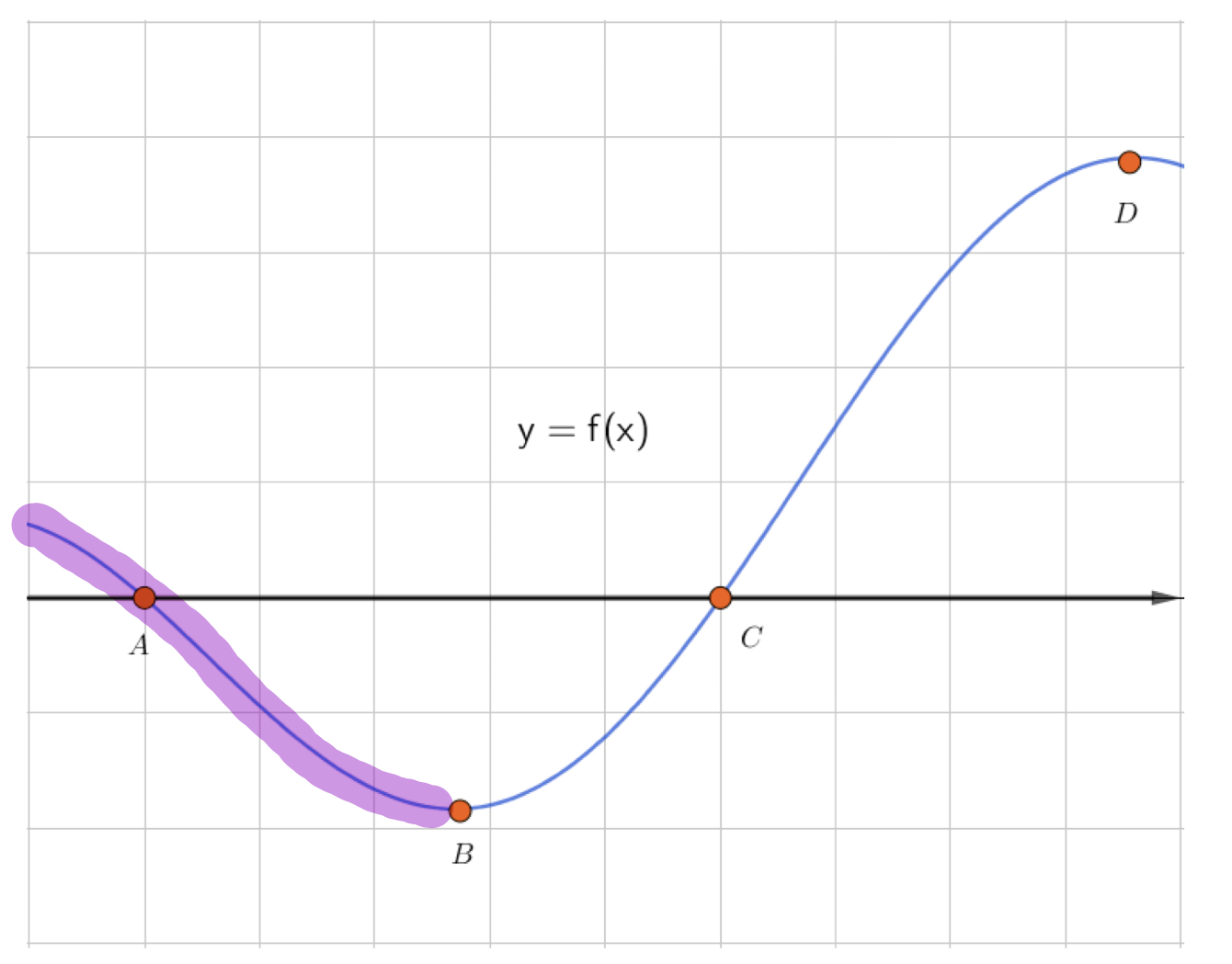
Промежуток, где производная положительна
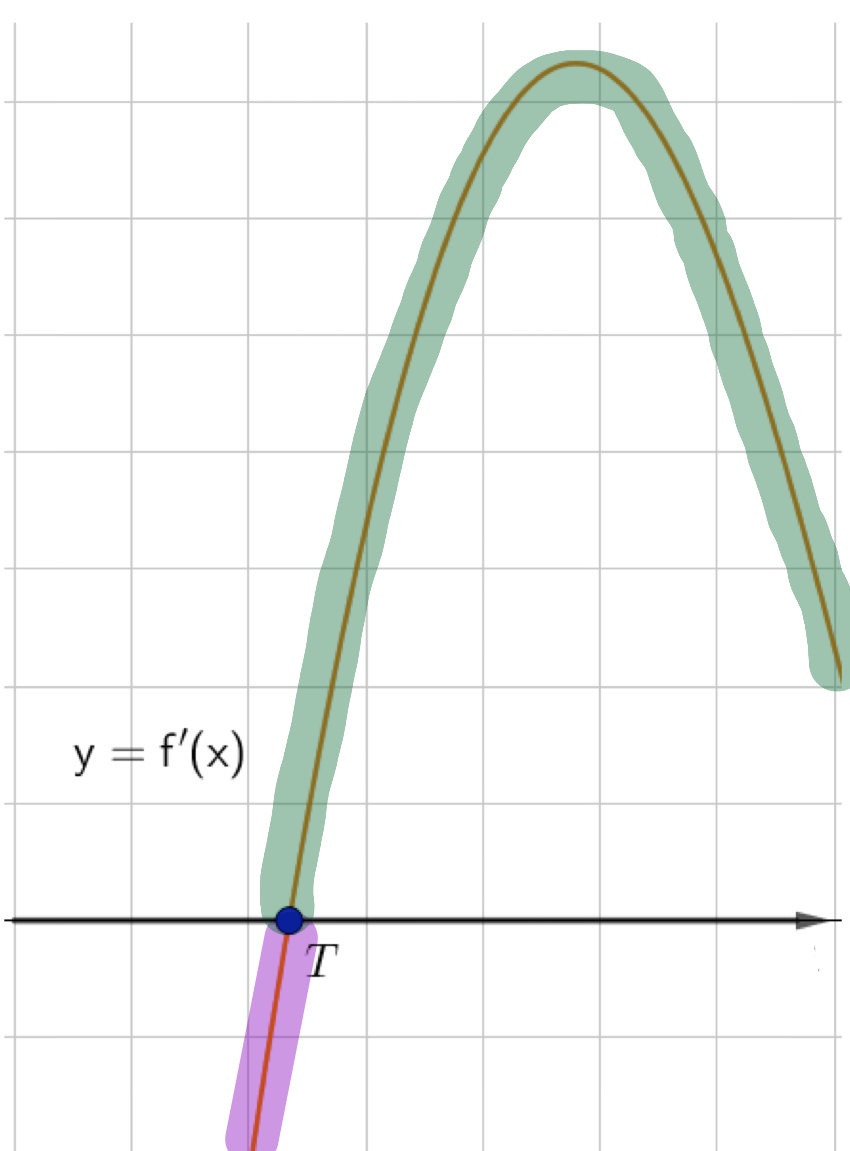
соответствует промежутку возрастания функции:
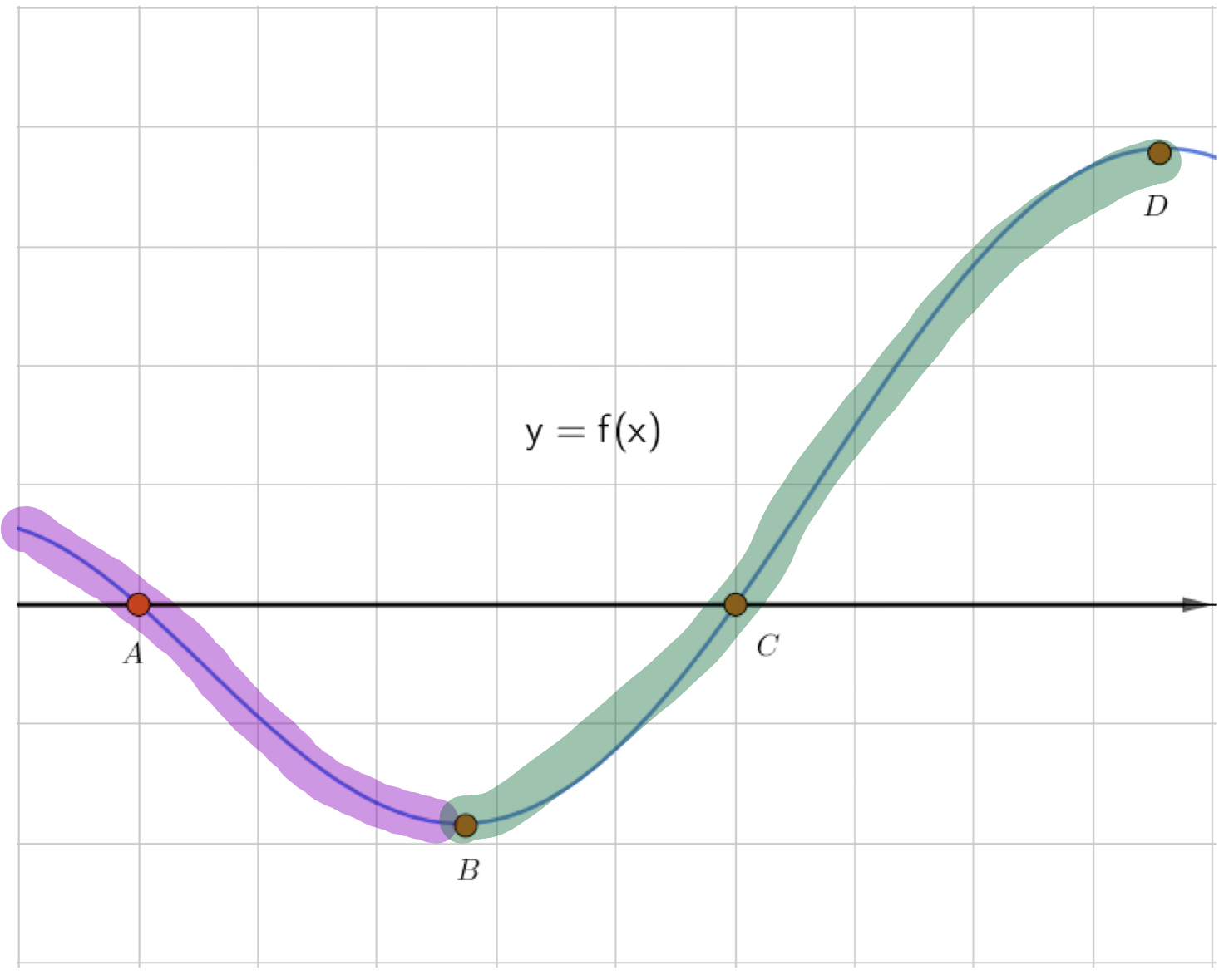
Таким образом, точка \(\displaystyle T\) графика \(\displaystyle y=f^{\prime}(x)\) соответствует точке локального минимума функции \(\displaystyle y=f(x){ \small ,}\) это точка \(\displaystyle B{\small .}\)
Ответ: точка \(\displaystyle B{\small .}\)