Определите знаки \(\displaystyle \cos\left(\frac{6\pi}{5}\right)\) и \(\displaystyle \sin \left(\frac{6\pi}{5}\right){\small:}\)
\(\displaystyle \cos \left(\frac{6\pi}{5}\right)\) и \(\displaystyle \sin\left(\frac{6\pi}{5}\right)\)
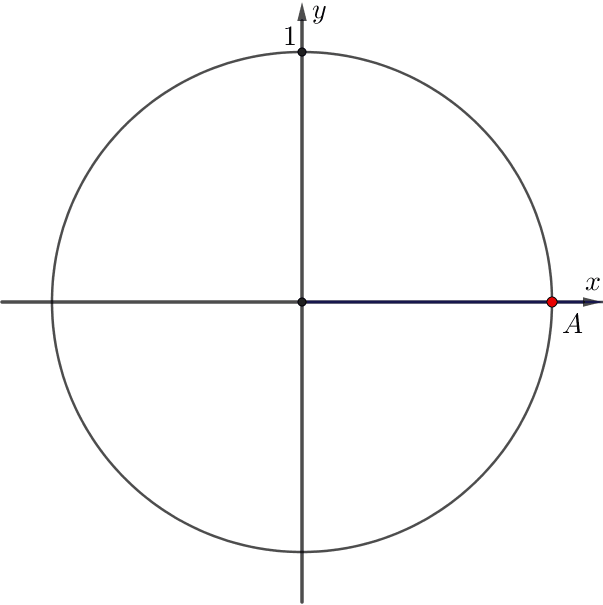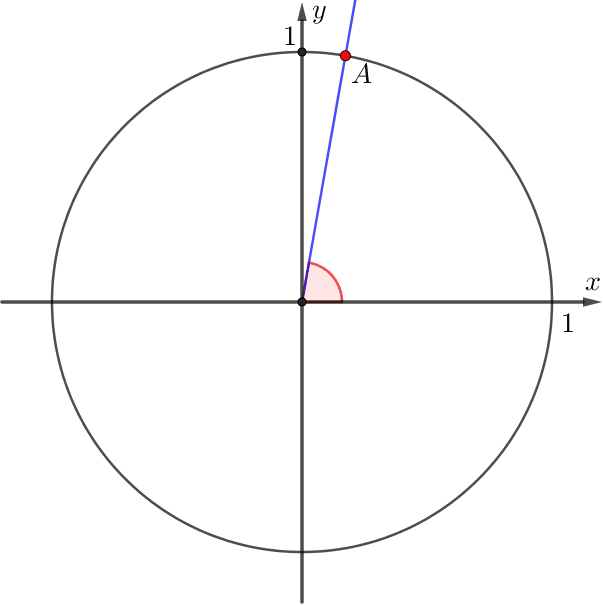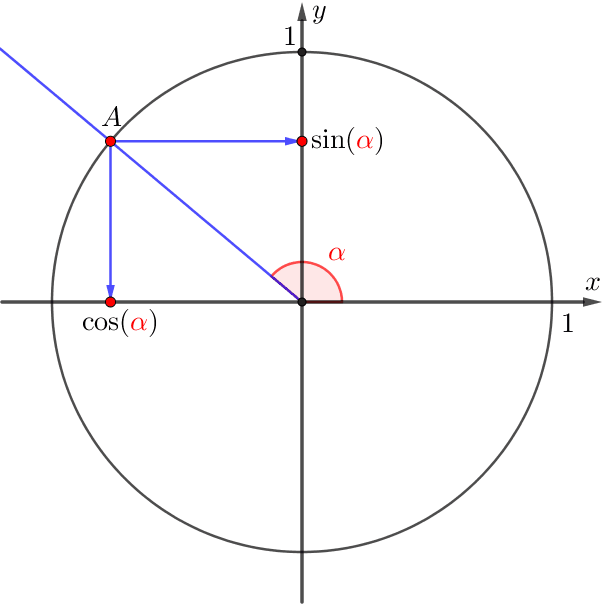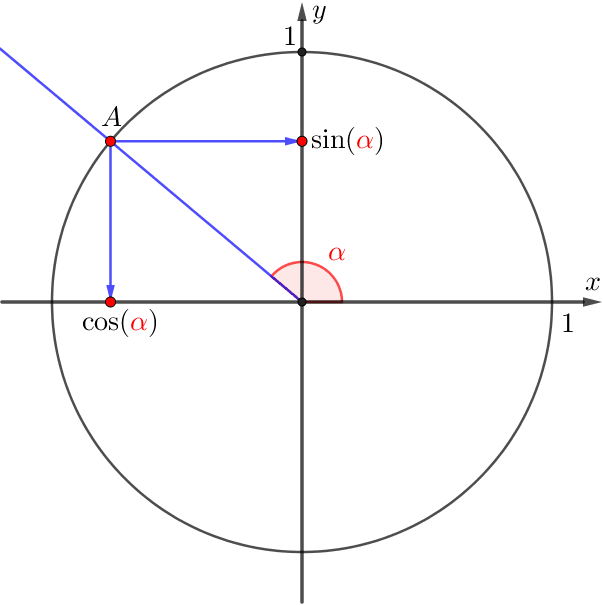
Воспользуемся определением синуса и косинуса угла.
Тогда \(\displaystyle \cos\left(\frac{6\pi}{5}\right)\) и \(\displaystyle \sin \left(\frac{6\pi}{5}\right)\) – это координаты точки, полученной поворотом луча на угол \(\displaystyle \frac{6\pi}{5}{\small .} \)
При этом, так как \(\displaystyle \frac{6\pi}{5}=\pi+\frac{\pi}{5}{ \small ,} \) то луч \(\displaystyle OA\) окажется в \(\displaystyle \rm III\) четверти:
Следовательно, абсцисса и ордината точки \(\displaystyle A\) отрицательны.
Значит,
- \(\displaystyle \cos\left(\frac{6\pi}{5}\right)<0{\small,}\)
- \(\displaystyle \sin\left(\frac{6\pi}{5}\right)<0{\small.}\)
Ответ: \(\displaystyle \cos\left(\frac{6\pi}{5}\right)<0\) и \(\displaystyle \sin \left(\frac{6\pi}{5}\right)<0{\small.}\)