Дана единичная окружность, на которой отмечена точка \(\displaystyle A{\small .} \) Определите координаты точки \(\displaystyle A{\small .} \)
Абсцисса точки \(\displaystyle A\) равна
Ордината точки \(\displaystyle A\) равна
Дана единичная окружность с центром в точке \(\displaystyle O{\small.}\) Точка \(\displaystyle A\) имеет координаты \(\displaystyle (1;0){\small .}\)
Луч \(\displaystyle OA\) повернулся на угол \(\displaystyle \color{red}{\alpha}{\small.}\)
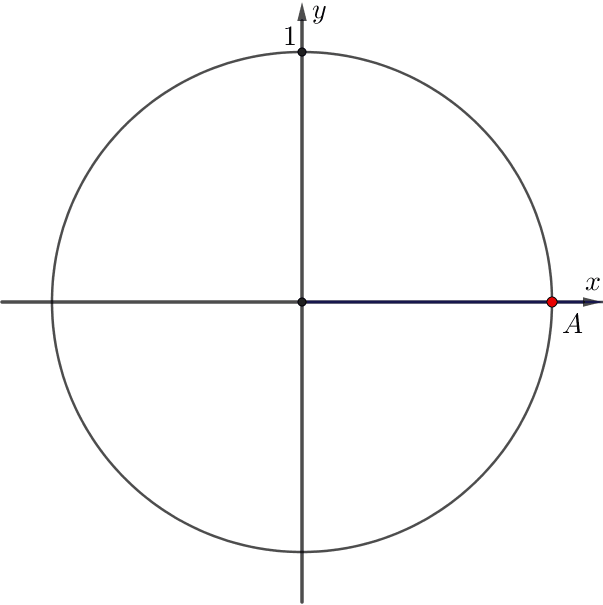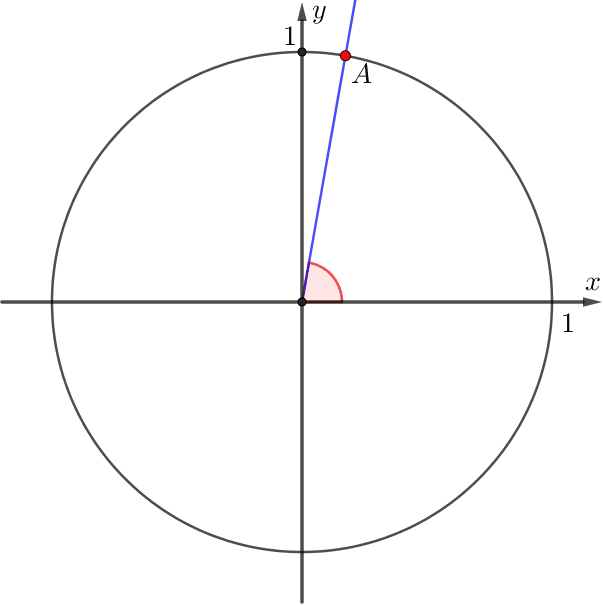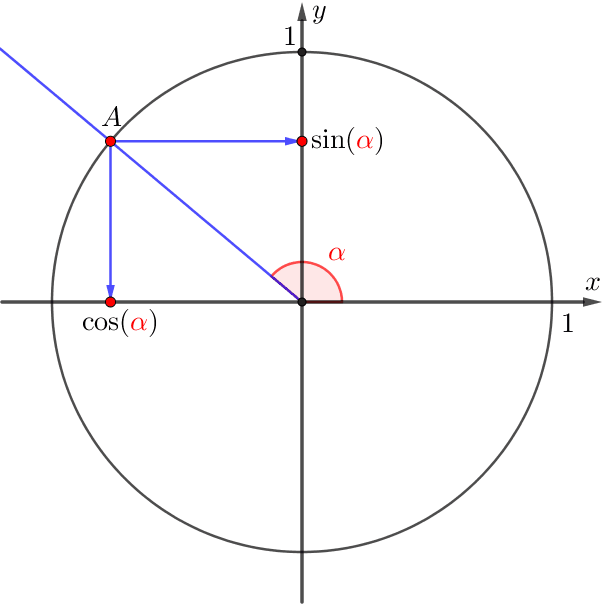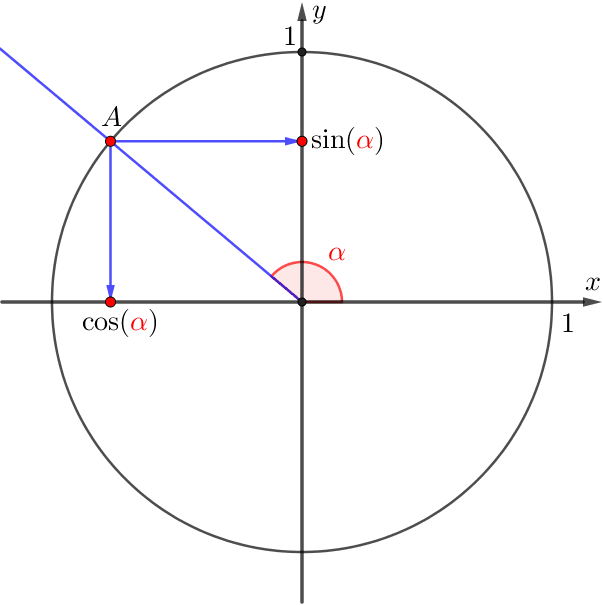
Тогда
- косинусом угла \(\displaystyle \color{red}{\alpha}\) называется абсцисса точки \(\displaystyle A\) и обозначается \(\displaystyle \cos(\color{red}{\alpha}){\small,}\)
- синусом угла \(\displaystyle \color{red}{\alpha}\) называется ордината точки \(\displaystyle A\) и обозначается \(\displaystyle \sin(\color{red}{\alpha}){\small.}\)
На рисунке, предложенном в условии, угол между положительным направлением оси \(\displaystyle \rm OX\) и лучом \(\displaystyle OA\) равен \(\displaystyle \frac{13\pi}{11}{\small.}\)
Значит, абсцисса точки \(\displaystyle A\) равна \(\displaystyle \cos\left(\frac{13\pi}{11}\right){\small,}\) ордината точки \(\displaystyle A\) равна \(\displaystyle \sin\left(\frac{13\pi}{11}\right){\small.}\) |