\(\displaystyle ABCD\) – ромб, \(\displaystyle O\) – точка пересечения его диагоналей \(\displaystyle AC\) и \(\displaystyle BD{\small.}\) Найдите длину отрезка \(\displaystyle AO{\small,}\) если сторона ромба равна \(\displaystyle 2\sqrt{3}\) и \(\displaystyle \angle BAO=30^{\circ}{\small.}\)
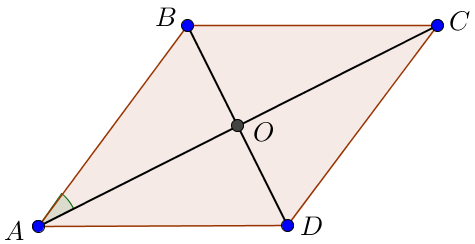

Поскольку в ромбе диагонали перпендикулярны, то угол \(\displaystyle AOB\) прямой.
Рассмотрим прямоугольный треугольник \(\displaystyle AOB {\small.}\)
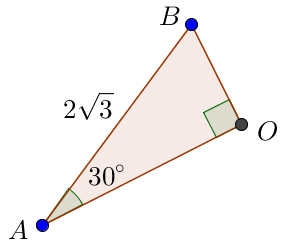
В прямоугольном треугольнике с острым углом \(\displaystyle 30^{\circ}\) катет, лежащий против угла \(\displaystyle 30^{\circ}{\small,}\) равен половине гипотенузы. Значит,
\(\displaystyle OB=\frac{1}{2}\cdot AB=\frac{1}{2}\cdot 2\sqrt{3}=\sqrt{3}.\)
По теореме Пифагора
\(\displaystyle AB^2=AO^2+OB^2.\)
Тогда
\(\displaystyle (2\sqrt{3})^2=AO^2+\left({\sqrt{3}}\right)^2,\)
\(\displaystyle 12=AO^2+{3},\)
\(\displaystyle AO^2=12-3=9.\)
Поскольку длина отрезка положительна, то
\(\displaystyle AO=\sqrt{9}={3}.\)
Ответ: \(\displaystyle 3{\small .}\)