Сторона ромба равна \(\displaystyle 5{\small.}\) Одна из его диагоналей на \(\displaystyle 2\) больше другой. Найдите меньшую диагональ.

Пусть \(\displaystyle BD=x\) – меньшая диагональ ромба, тогда \(\displaystyle AC=x+2 \) – большая диагональ ромба.

По свойству параллелограмма диагонали точкой пересечения делятся пополам. Значит,
\(\displaystyle BO=OD=\frac{x}{2}\) и \(\displaystyle AO=OC=\frac{x+2}{2}{\small.}\)
По свойству ромба диагонали перпендикулярны. Значит, угол \(\displaystyle AOB\) – прямой.
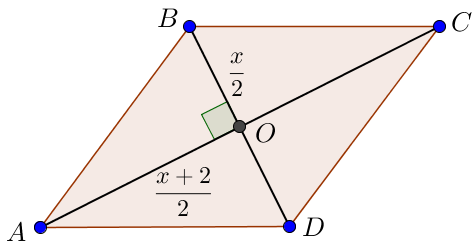
Выразим сторону \(\displaystyle AB\) ромба из прямоугольного треугольника \(\displaystyle AOB{\small.}\) По теореме Пифагора
\(\displaystyle AB^2=AO^2+OB^2{\small.}\)
Тогда
\(\displaystyle {5}^2=\left(\frac{x+2}{2}\right)^2+\left(\frac{x}{2}\right)^2{\small,}\)
\(\displaystyle 25=\frac{x^2+4x+4}{4}+\frac{x^2}{4}{\small,}\)
\(\displaystyle 100=2x^2+4x+4{\small,}\)
\(\displaystyle 2x^2+4x-96=0{\small,}\)
\(\displaystyle x^2+2x-48=0{\small.}\)
Решим квадратное уравнение.
Так как длина отрезка положительна, то \(\displaystyle x=6.\) Следовательно, длина меньшей диагонали ромба равна \(\displaystyle 6{\small.}\)
Ответ: \(\displaystyle 6{\small .}\)