Задание
Правило
Для любых чисел \(\displaystyle a,\, b\) и \(\displaystyle c\) верно, что
\(\displaystyle a+(b+c)=a+b+c{\small .}\)
Решение
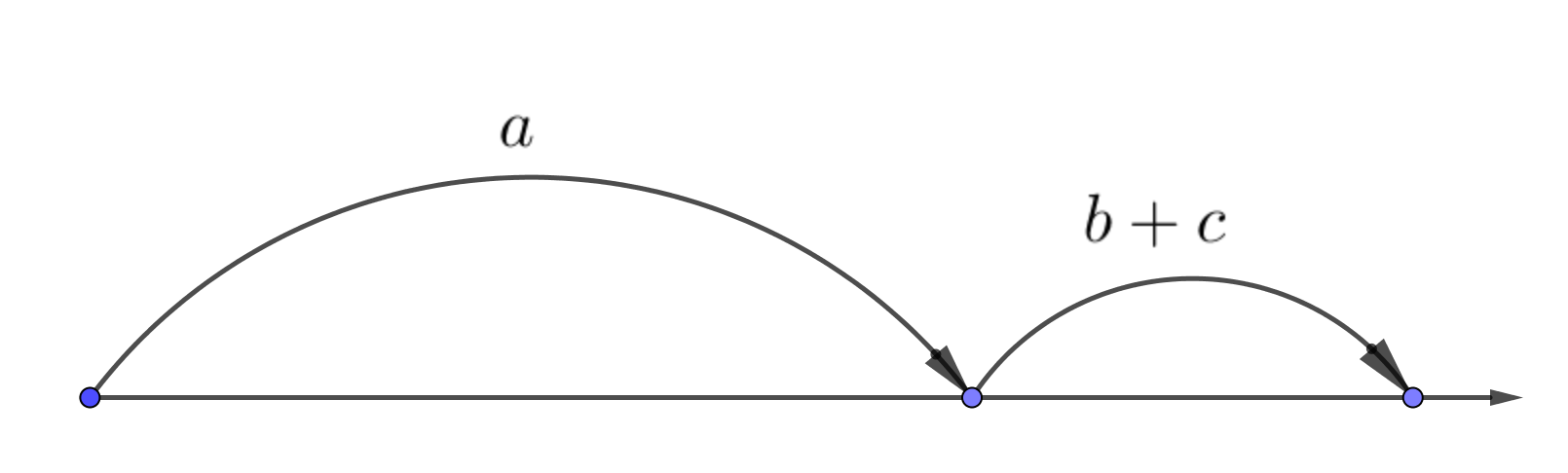
Построение отрезка длины \(\displaystyle a+(b+c){\small .}\)

На диаграмме показано построение отрезка длины \(\displaystyle a+(b+c){\small .}\)
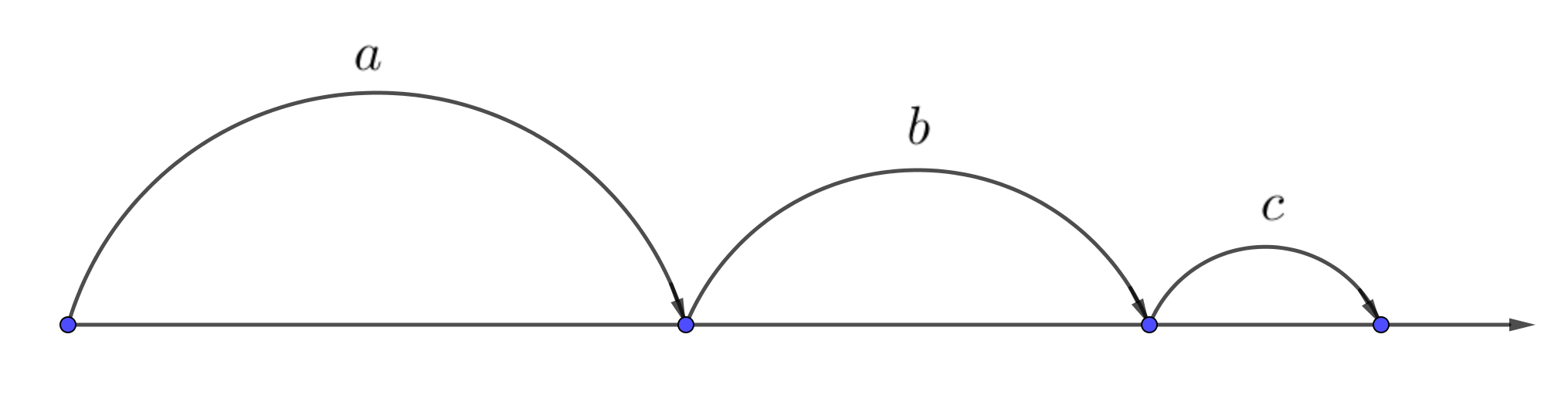
Построение отрезка длины \(\displaystyle a+b+c{\small .}\)

На диаграмме показано построение отрезка длины \(\displaystyle a+b+c{\small .}\)
\(\displaystyle a+(b+c)=a+b+c\) opened="1
 |  | |
| \(\displaystyle a+(b+c)\) | \(\displaystyle =\) | \(\displaystyle a+b+c\) |
Таким образом, получаем
\(\displaystyle a+(b+c)=a+b+c\)
для любых \(\displaystyle a,\, b\) и \(\displaystyle c.\)