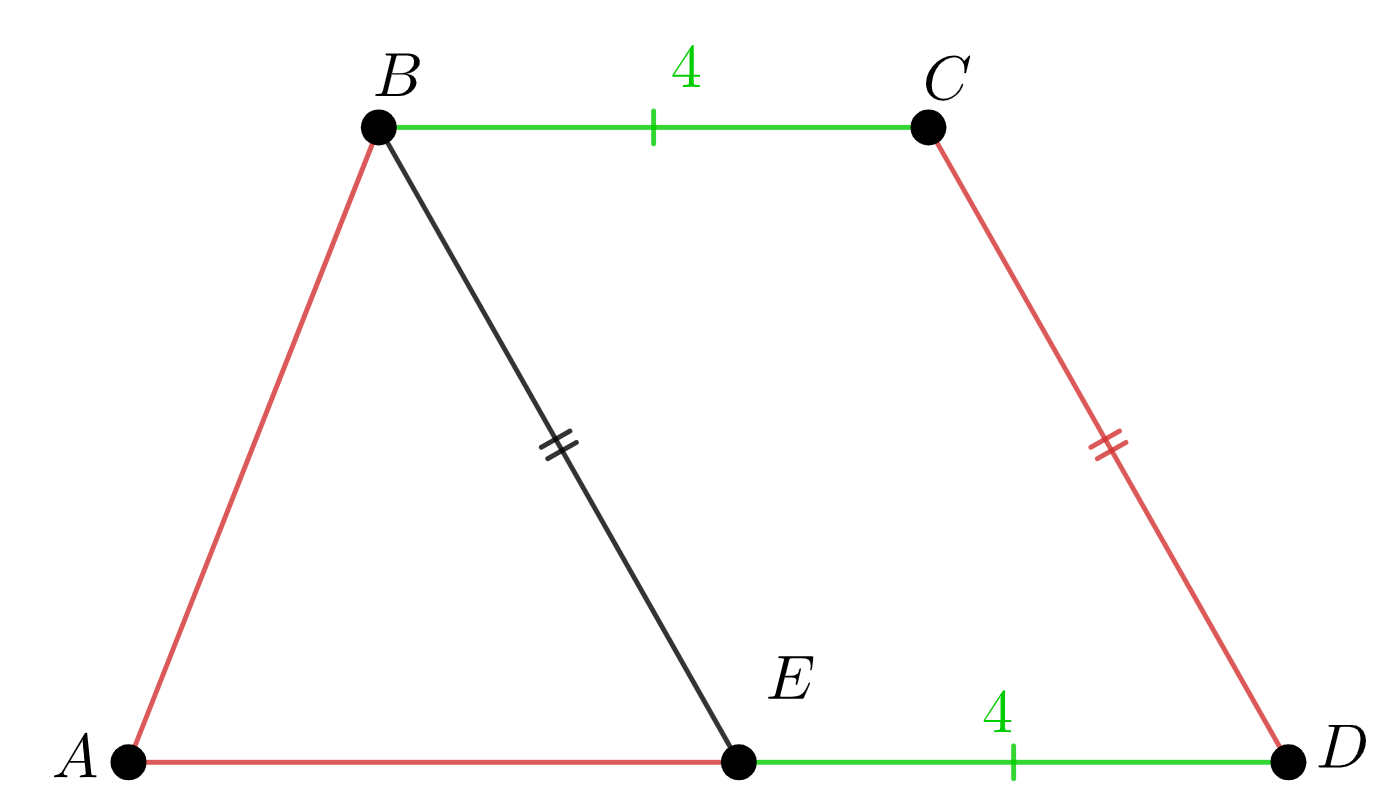
В трапеции \(\displaystyle ABCD\) меньшее основание \(\displaystyle BC\) равно \(\displaystyle 4{\small ,}\) прямая \(\displaystyle BE\) параллельна боковой стороне \(\displaystyle CD{\small .}\) Найдите периметр трапеции \(\displaystyle ABCD{\small ,}\) если периметр треугольника \(\displaystyle ABE\) равен \(\displaystyle 15{\small .}\)
Рассмотрим четырехугольник \(\displaystyle BCDE{\small .}\) В нём: \(\displaystyle BE\parallel CD\) по условию, \(\displaystyle BC\parallel ED\) как прямые, содержащие основания трапеции. Значит, \(\displaystyle BCDE\) – параллелограмм. Следовательно, \(\displaystyle BC=ED\)и \(\displaystyle BE=CD\small.\) |  |
Требуется найти периметр трапеции \(\displaystyle ABCD{\small .}\) \(\displaystyle P_{ABCD}=AB+BC+CD+DA \small.\) По условию \(\displaystyle \color{green}{BC}=\color{green}{ED}=\color{green}{4}\small,\) \(\displaystyle \color{red}{P_{\triangle ABE}}=\color{red}{AB}+\color{red}{BE}+\color{red}{AE}=\color{red}{15}\small.\)
| 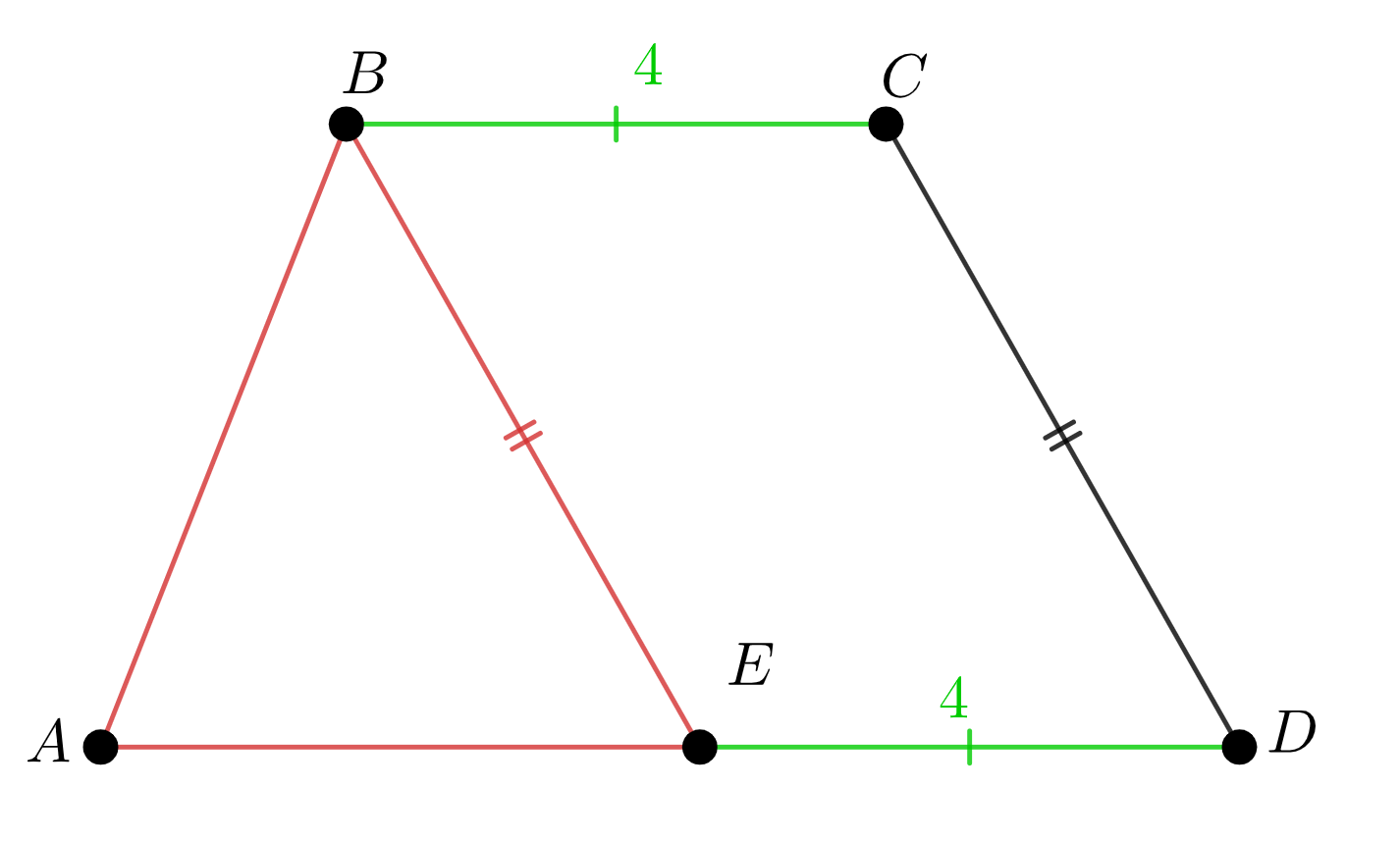 |
Поскольку \(\displaystyle \color{red}{BE}=\color{red}{CD}\) и \(\displaystyle DA=\color{red}{AE}+\color{green}{ED} \small,\) то
\(\displaystyle P_{ABCD}=\color{red}{AB}+\color{green}{BC}+\color{red}{CD}+\color{red}{AE}+\color{green}{ED} \small. \) То есть \(\displaystyle \begin{aligned} P_{ABCD}&=\color{red}{P_{\triangle ABE}}+\color{green}{BC}+\color{green}{ED}=\\ &=\color{red}{15}+\color{green}{4}+\color{green}{4}=23{\small .} \end{aligned}\) |
|
Ответ: \(\displaystyle 23{\small .}\)